Spaced Repetition Algorithm: A Three‐Day Journey from Novice to Expert

I am Jarrett Ye, the principal author of the paper A Stochastic Shortest Path Algorithm for Optimizing Spaced Repetition Scheduling and the paper Optimizing Spaced Repetition Schedule by Capturing the Dynamics of Memory. I currently serve at MaiMemo Inc., where I am chiefly responsible for developing the spaced repetition algorithm within MaiMemo's language learning app. For a detailed account of my academic journey leading to the publication of these papers, please refer to: How did I publish a paper in ACMKDD as an undergraduate?

This tutorial, "Spaced Repetition Algorithms: A Three-Day Journey from Novice to Expert," is adapted from the manuscript I initially prepared for internal presentations at MaiMemo. The objective is to elucidate what exactly spaced repetition algorithms are investigating, and to inspire a new cadre of researchers to contribute to this field and advance the progress of learning technology. Without further ado, let us embark on this intellectual journey.

Preface

From our school days, most students have two simple intuitions:

1. Review information multiple times helps us remember it better.
2. Different memories fade at different rates, not all at once.

These insights raise further questions:

1. How much knowledge have we already forgotten?
2. How quickly are we forgetting them?
3. What is the best way to schedule reviews to minimize forgetting?

In the past, few people have measured these factors or used them to optimize their review schedules. The focus of spaced repetition algorithms is to understand and predict how we remember things and to schedule our reviews accordingly.

In the next three days, we will delve into spaced repetition algorithms from three perspectives:

1. Empirical Algorithms
2. Theoretical Models
3. Latest progresses

Day 1: Exploring Empirical Algorithms

Today we begin our journey by diving into the simplest yet impactful empirical algorithms. We'll uncover the details and the ideas that guide them. But first, let's trace the roots of a term that pervades this field—Spaced Repetition.

Spaced Repetition

For readers new to the subject of spaced repetition, let's learn about the concept of the "forgetting curve."

After we first learn something, whether it's from a book or a class, we start to forget it. This happens gradually, just like the forgetting curve that slopes downward.

The forgetting curve provides an illustration of the way our memory retains knowledge. It exhibits a unique trajectory: in the absence of active review, the decay of memory is initially swift, and slow down over time.

How can we counteract this natural propensity to forget? Let's consider the power of review.

Introducing periodic reviews results in a flattened forgetting curve, indicating a slower decay of memory over time.

In the period following the assimilation of new information, when we undertake a review and characterize our retention with an updated forgetting curve, we find that the curve has become flatter. This indicates that the rate at which we forget has slowed down.

So how should one optimize these review intervals for enhanced memory retention?

Notice the varying lengths of the review intervals? Shorter intervals are used for unfamiliar content, while longer ones are employed for more familiar material, which scatter reviews over different timings in the future. This tactic, known as Spaced Repetition, augment long-term memory retention.

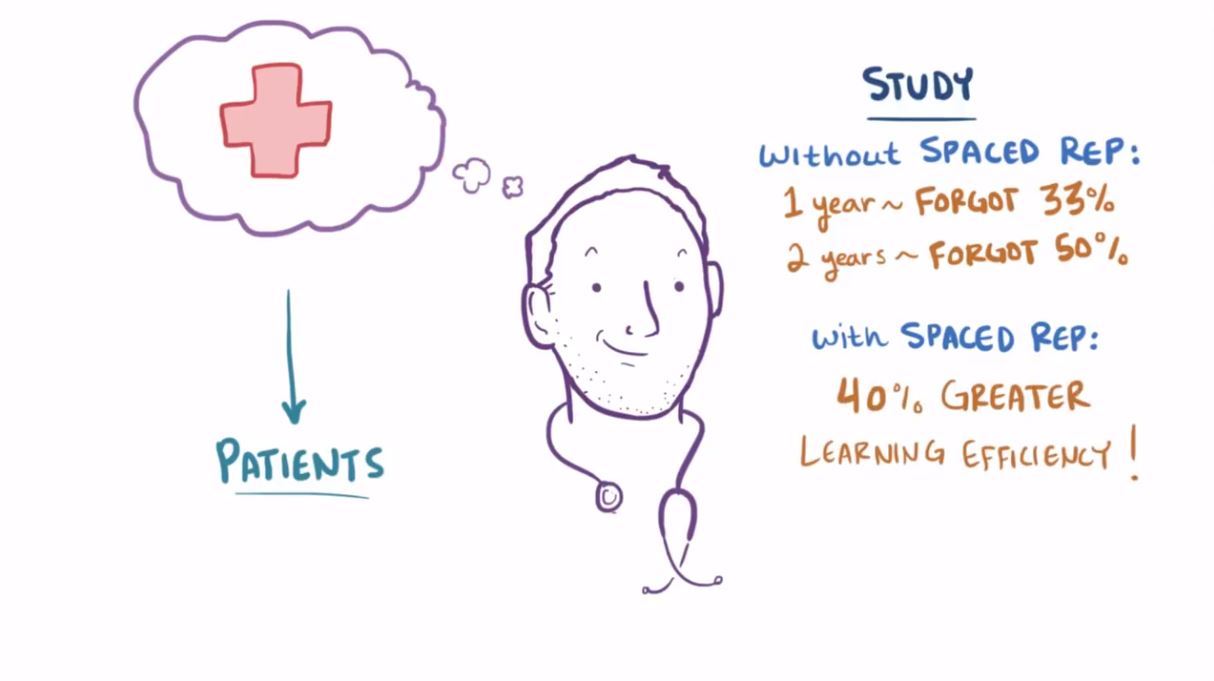
But how effective is it? Let's examine some stats from medical students.

Without Spaced Repetition, students forget 33% of the material after one year and 50% after two years. With Spaced Repetition, however, learning efficiency spikes by 40%.

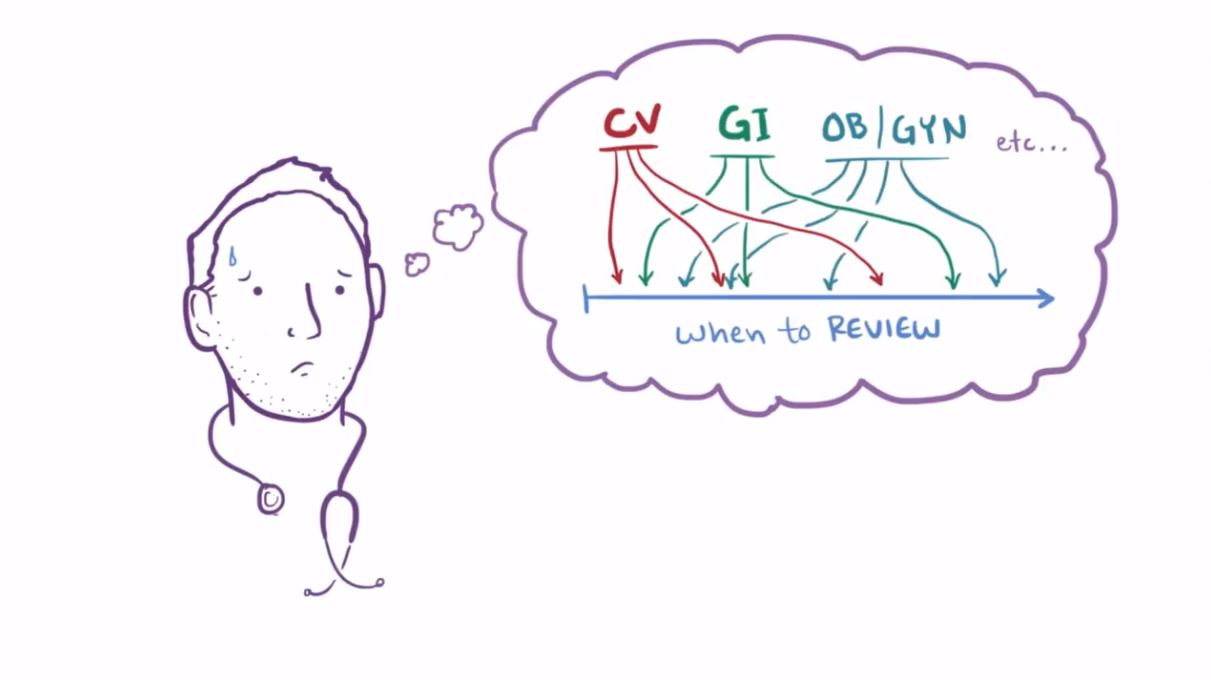
If Spaced Repetition is so impactful, why hasn't it gained mass adoption?

The obstacle lies in the overwhelming volume of knowledge to learn. Each piece of knowledge has its unique forgetting curve, making manual tracking and scheduling a impossible mission.

This introduces the role of spaced repetition algorithms: automating the tracking of memory states and arrange efficient review schedules.

By now, you should have a basic understanding of Spaced Repetition. But questions likely still linger, such as optimal review timing and best practices for efficient Spaced Repetition. The answers to these await in the coming chapters. Let's move on to the heart of the matter!

Review Section

Question	Answer
What aspect of memory does the forgetting curve capture?	The curve describes how knowledge retention decays over time in our memory.
How does memory retention decline when review is not engaged?	It decreases swiftly initially and then slows down.
After a successful review, what distinguishes the new forgetting curve from its predecessor?	The new curve is flatter, indicating a slower rate of forgetting.
What features are specific to the timing of reviews in spaced repetition?	Reviews are distributed over multiple future timings.
How does spaced repetition accommodate content of different familiarity levels?	Shorter intervals are applied for unfamiliar content, while longer ones are set for familiar material.
What function do algorithms serve in spaced repetition?	They automate the tracking of memory states and the arrangement of efficient review schedules.

---

Having delved into the concept of spaced repetition, you may now be pondering this guiding principle:

Shorter intervals are used for unfamiliar content, while longer ones are employed for more familiar material, which scatter reviews over different timings in the future.

What exactly defines these 'short' or 'long' intervals? Furthermore, how can one distinguish between material that is 'familiar' and that which is 'unfamiliar'?

Intuitively, the slower the material is forgotten in our memory, the more familiar it is. And a reasonable interval should minimize our forgetting. But the less we want to forget, the shorter the interval we can deduce from the forgetting curve. The shorter the interval, the higher the frequency of review.

It seems there's an inherent contradiction between the frequency of review and the rate of forgetting—how to reconcile this discrepancy?

Sitting in front of the computer and daydreaming, it seems that no conclusions can be drawn. We still know too little about spaced repetition.

If you were to resolve this conflict, what would you need to continue to learn? What kind of experiment would you design? Keep thinking about them, and even better, write them down!

Let's take a look at how the creator of the first computational spaced repetition algorithm set out on his journey in the exploration of memory.

SM-0

In 1985, a young college student named Peter Wozniak (aka Woz) was struggling with the problem of forgetting:

The above image shows a page from his vocabulary notebook, which contained 2,794 words spread across 79 pages. Each page had about 40 pairs of English-Polish words. Managing their review was a headache for Wozniak. At first, he didn't have a systematic plan for reviewing the words; he just reviewed whatever he had time for. But he did something crucial: he kept track of when he reviewed and how many words he forgot, allowing him to measure his progress.

He compiled a year's worth of review data and discovered that his rate of forgetting ranged between 40% and 60%. This was unacceptable to him. He needed a reasonable study schedule that would lower his forgetting rate without overwhelming him with reviews. To find an optimal review interval, he commenced his own memory experiments.

Wozniak wanted to find the longest possible time between reviews, while keeping the forgetting rate under 5%.

Here are the details about his experiment:

Materials: Five pages of English-Polish vocabulary, each with 40 word pairs.

Initial Learning: Memorize all 5 pages of material. The specific operation is: look at the English, recall the Polish, and then check whether the recall is correct. If the recall is correct, eliminate the word pair from this phase. If the recall fails, try to recall it later until all the memories are correct.

Initial Review: A one-day interval was employed for the first review, based on Woz's previous review experience.

The ensuing key phases—A, B, and C—revealed the following:

Phase A: Woz reviewed five pages of notes at intervals of 2, 4, 6, 8, and 10 days. The resulting forgetting rates were 0%, 0%, 0%, 1%, and 17%, respectively. He determined that a 7-day interval was optimal for the second review.

Phase B: A new set of five pages was reviewed after 1 day for the first time, and then after 7 days for the second time. For the third review, the intervals were 6, 8, 11, 13, and 16 days, with forgetting rates of 3%, 0%, 0%, 0%, and 1%. Wozniak selected a 16-day interval for the third review.

Phase C: Another fresh set of five pages was reviewed at 1, 7, and 16-day intervals for the first three reviews. For the fourth review, the intervals were 20, 24, 28, 33, and 38 days, with forgetting rates of 0%, 3%, 5%, 3%, and 0%. Wozniak opted for a 35-day interval for the fourth review.

Subsequently, Woz conducted experiments to identify the optimal interval for the fifth review. However, the time required for each successive phase was approximately double that of the preceding one. Ultimately, he formalized the SM-0 algorithm on paper.

• I(1) = 1 day
• I(2) = 7 days
• I(3) = 16 days
• I(4) = 35 days
• for i>4: I(i) = I(i-1) * 2
• Words forgotten in first four reviews were moved to a new page and cycled back into repetition along with new materials.

In this context, $I(i)$ denotes the interval employed for the $i^{th}$ review. The interval for the fifth repetition was set to be twice that of the preceding one, a stipulation grounded in intuitive assumptions. Over the two years of utilizing the SM-0 algorithm, Woz collected sufficient data to corroborate the validity and accuracy of this hypothesis.

The goal of the SM-0 Algorithm was clear: to extend the review interval as much as possible while minimizing the rate of memory decay. Its limitations were evident as well, namely its inability to track memory retention at a granular level.

Nonetheless, the significance of the SM-0 Algorithm was far-reaching. With the acquisition of his first computer in 1986, Woz simulated the model and drew two key conclusions:

• Total knowledge retention could increase over time.
• The learning rate remained relatively stable in the long term.

These insights proved that the algorithm could reconcile the tension between memory retention and the frequency of review. Woz realized that spaced repetition didn't have to mire learners in a cycle of endless review, thereby inspiring him to continue refining spaced repetition algorithms.

Review Section

Questions	Answers
Which two factors did Woz consider for determining optimal review intervals?	Interval duration, which is linked to the frequency of review, and the rate of memory decay, associated with memory retention.
Why did Woz use new materials each time he sought to establish a new review interval in his experiments?	To ensure uniformity in the intervals of prior reviews, thus controlling for variables.
What is the primary limitation of the SM-0 Algorithm?	It uses a page of notes as the unit for review, making it unsuitable for tracking memory retention at a more granular level.

SM-2

Though the SM-0 algorithm displayed initial efficacy, several issues prompted Wozniak to seek refinements:

1. If a word is forgotten during the first review (after 1 day), it will be easier to forget again in the second and third reviews (after 7 and 16 days) compared to words that were not forgotten before.

2. Pages of new notes made up of words forgotten after the fourth review have a higher forgetfulness rate under the same review schedule.

The first finding made him realize that reviewing doesn't always make him more familiar with the material. Forgotten stuff gets even more unfamiliar, and the speed of forgetting doesn't slow down. If he keeps reviewing these words with longer gaps like the rest on the same note page, it won't work well.

The second finding made him see that not all material is equally hard. Different difficulty levels should have different review gaps.

Consequently, in 1987, armed with his initial personal computer, Woz utilized his two-year record and insights from the SM-0 algorithm to craft the SM-2 algorithm.

The details about SM-2:

• Break down the information you want to remember into small question-answer pairs.
• Use the following gaps (in days) to repeat each question-answer pair:

  • $I(1) = 1$

  • $I(2) = 6$

  • For $n > 2$, $I(n) = I(n-1) \times EF$

    • $EF$—the Ease Factor, with an initial value of 2.5
    • After each review, $\text{newEF} = EF + (0.1 - (5-q) \times (0.08 + (5-q) \times 0.02))$
      • $\text{newEF}$—the post-review updated value of the Ease Factor
      • $q$—the quality grades of review, ranging from 0 - 5. If it's >= 3, it means the learner remembered, and if it's < 3, the learner forgot.

  • If the learner forgets, the interval for the question-answer pair will be reset to $I(1)$ with the the same EF.

The SM-2 algorithm adds the review feedback into how often you review the question-answer pairs. This feedback kinda shows how hard or easy they are. The lower the EF, the smaller the interval multiple factor.

The SM-2 algorithm still relies on Woz's own experimental data, but two main updates make it a popular spaced repetition algorithm today:

1. It breaks down the notes page into smaller question-answer pairs. This lets the review schedule be super specific to each pair and separates out the hard and easy stuff sooner.

2. It uses an "Ease Factor" and grades. So, the algorithm can modify the learner's future reviews based on how well the learn remembers.

Review Section

Questions	Answers
Why shouldn't we set a longer interval for stuff we forgot during review?	The speed of forgetting for those things doesn't slow down.
What shows that some stuff is harder to remember than others?	The pages with stuff that got forgotten have a higher rate of being forgotten again.
What is the functional utility of incorporating an "Ease Factor" and "Quality Grade" into the SM-2 algorithm?	This enables the algorithm to dynamically adjust future review intervals based on user performance.
What are the advantages of breaking down note pages into smaller parts for review?	It lets the algorithm sort out the easier and harder stuff sooner for when to review them next.

SM-4

The primary objective of SM-4 is to address the shortcomings in adaptability found within its predecessor, the SM-2 algorithm. While SM-2 has the capacity to tune review schedules for individual flashcards based on ease factors and recall grades, these adjustments are made in isolation, without regard to prior alterations made to other cards.

In other words, each flashcard is treated as an independent entity in SM-2, leaving the algorithm perpetually uninformed about the user's overall learning process, regardless of the quantity of cards reviewed. To overcome this, SM-4 introduces an Optimal Interval Matrix, replacing the existing formulae used for interval calculations:

The matrix above is called the Optimal Interval (OI) matrix. It has rows for how easy stuff is and columns for how many times you've seen it. It starts the same as SM-2, using the same formulas to decide how long to wait before looking at a card again.

To make new cards learn from what happened with old cards, the OI matrix keeps changing as the learner reviews. The main idea is: if the OI matrix says to wait X days and the learner actually waits X+Y days and still remembers with a high grade, then the OI value should be changed to something between X and X+Y.

The reason for this is simple: if the learner can remember something after waiting X+Y days and get a good score, then the old OI value was probably too short. Why not make it longer?

This naive idea allows SM-4 to be the first algorithm capable of making holistic adjustments based on the learner's experience. But, it didn't work as well as hoped. The reasons are simple:

1. Each review only changes one entry of the matrix, so it takes too long to really make the OI matrix better.
2. For longer review interval, it takes a long time to make them stable.

To address these issues, the SM-5 algorithm was designed. But I won't go into details here because of space limits.

Review Section

Question	Answer
What accounts for the limited adaptability of SM-2?	Adjustments are made to each flashcard in isolation, precluding the sharing of experiential insights.
What components does SM-4 introduce to enhance adaptability?	Optimal Interval Matrix and dynamic interval-adjustment rules.
What is the underlying principle for interval adjustments in SM-4?	If the learner exhibits proficient recall over extended intervals, the original interval should be longer, and vice versa.

Summary

Invented in 1885, the Forgetting Curve shows how we remember and forget. Fast-forward to 1985, the computational spaced repetition aimed to find the optimal review schedule. This section has outlined the developmental progression of empirically based algorithms:

• SM-0 gathered experimental data to determine the best review intervals for a given individual and a specific type of material (Woz defined what "best" means here).
• SM-2 digitalized the algorithm for computer applications, introducing more granular card level and incorporating adaptive ease factors and recall grades.
• SM-4 further enhanced the adaptability of the algorithm for a diverse range of learners, introducing the Optimal Interval Matrix along with rules for adjusting the intervals.

While empirical algorithms offer a valuable lens through which to understand Spaced Repetition, it's really hard to make it better without a systematic theoretical underpinning. So, hang on! We're speeding up and diving into the theory part next!

Day 2: Understanding Theoretical Models

Memory algorithms sound like a theoretical study, but I've spent a lot of space on empirical algorithms. Why?

Because memory algorithms are an artificial science. Although memory is a natural phenomenon of human physiology, regular review to enhance memory is a strategy constructed by humans ourselves.

Without the foundational support of empirical approaches, any theoretical discourse would be without merit. The gut feelings we have about theory come from real-world experience.

So, the theories we'll talk about next will also start from what we've learned by doing. No building castles on sand here!

Two Components of Memory

Here's a question to think about: What factors would you consider when describing the state of something in your memory?

Before Robert A. Bjork, many researchers used memory strength to talk about how well people remembered something.

Do you think memory strength is enough to describe how well you remember something?

Let's revisit the Forgetting Curve for a moment:

First and foremost, Memory Retention (Recall Probability) clearly emerges as a pivotal variable in characterizing the state of one's memory. Derived from our quotidian experiences, forgetting often manifests as a stochastic phenomenon. No one can unequivocally assert that a word memorized today will be retained ten days hence or forgotten twenty days later.

Is recall probability sufficient for description? Imagine drawing a horizontal line across these Forgetting Curves; each curve will intersect at a point with identical recall probabilities. Have you noticed that recall probability alone seems insufficient for differentiating the conditions at these intersections?

Precisely, solely relying on recall probability does not allow us to distinguish the rate of forgetting associated with different materials. While this rate should certainly be factored into the description of memory states, it's a variable that changes with time. Can we depict it through a temporal-independent metric?

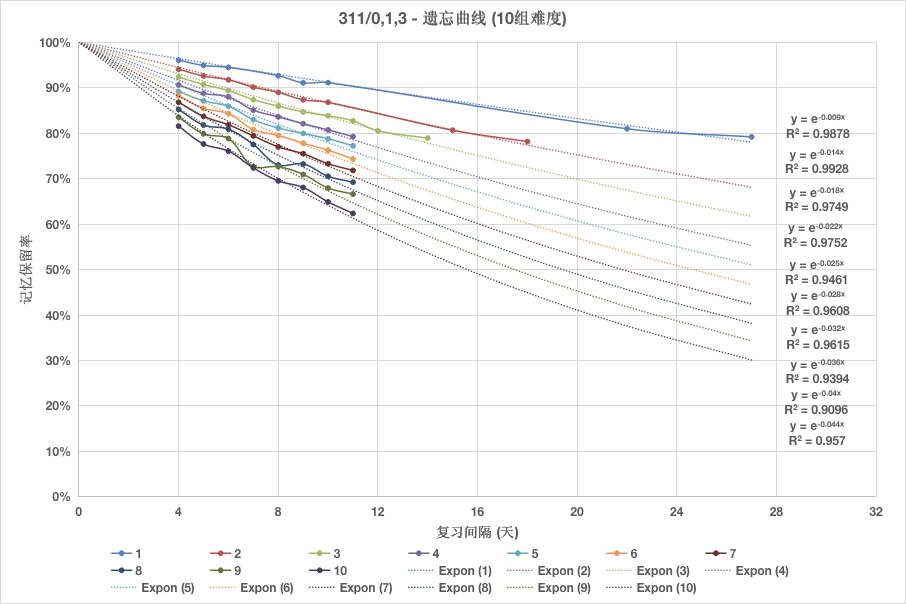
To address this quandary, we must delve into the mathematical properties of the forgetting curve—a task that necessitates the gathering of extensive data to plot the curve. The data, in this tutorial, is sourced from an open dataset created from language learning application MaiMemo.

From the figure above, we find that the forgetting curve approximates a negative exponential function with a base of $e$. The rate of forgetting can be captured by the corresponding decay constant of this function.

Considering that this decay constant is difficult to relate to the function image, we tend to transform this decay constant to obtain a fitting formula for the forgetting curve:

$$ \begin{aligned} R = \exp\left[\frac{t \ln{0.9}}{S}\right] \end{aligned} $$

In this equation, $R$ symbolizes the Probability of Recall, $S$ denotes the Memory Stability, and $t$ accounts for the time that has elapsed since the last review.

The correlation between $S$ and the shape of forgetting curve is displayed in the following figure:

The notion of "Memory Stability," $S$, corresponds precisely to the duration required for the "Probability of Recall," $R$, to decline from 100% to 90%. (In alternative scholarly literature, a 50% benchmark is often employed, in which case the stability is referred to as the memory's half-life.)

The two strengths of memory proposed by Bjork's - retrieval strength and storage strength - corresponds precisely to recall probability and memory stability.

The equation embodies three distinct properties:

1. When $t=0$, $R=100%$, signifying that upon immediate review, the process of forgetting has not yet been initiated, rendering the Probability of Recall at a maximal level.

2. As $t$ approaches infinity, $R$ converges toward zero, indicating that if you never review something, you will forget almost all of them.

3. The first derivative of the negative exponential function is diminishing, aligning with the empirical observation that forgetting is fast initially and slow down subsequently.

Thus, we have delineated two integral components of memory, but seems like something's missing.

The Probability of Recall quantifies the extent of forgetting, while Memory Stability characterizes the rate of forgetting; what else is not described?

Well, the moment when the shape of forgetting curve changes! The memory stability changes, and it doesn't only rely on the Probability of Recall at review and its previous Memory Stability.

Is there evidence to substantiate this claim? Think about the first time you learn something: your memory stability and probability of recall are both zero. But after you learn it, your probability of recall is 100%, and the memory stability depends on a certain property of the stuff you just learned.

Basically, the thing you're trying to remember itself has some features that can affect your memory. Intuitively, this variable is the difficulty of material.

With this variable of difficulty added, we now have a three-components model to describe memory.

Review Section

Question	Answer
Why can't a single variable of memory strength adequately describe the state of memory?	A single variable is insufficient because the forgetting curve encompasses both retention levels and the rate of forgetting.
What variable measures the degree of memory retention?	Recall Probability
Which function can approximate the forgetting curve?	Exponential Function
What variable measures the speed of memory degradation?	Decay Constant
What is the practical implication of memory stability?	The time required for the recall probability to decline from 100% to a predetermined percentage, often 90%.

The Three Component Model of Memory

Let us delve directly into the terminological conventions:

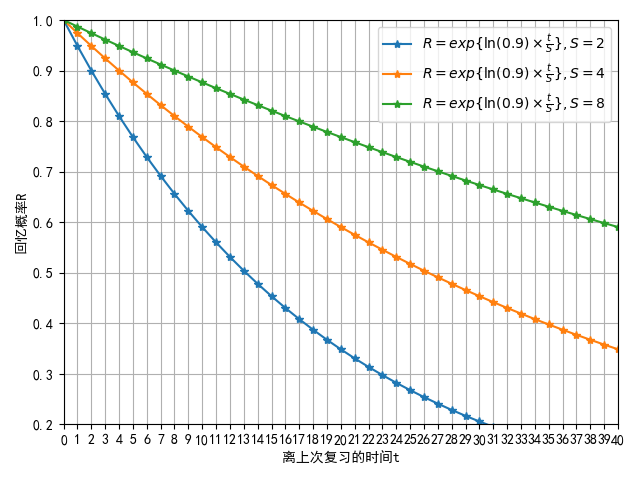
• Memory Stability: The duration required for the probability of recall for a particular memory to decline from 100% to 90%.
• Memory Retrievability: The probability of recalling a specific memory at a given moment.
• Intrinsic Memory Difficulty: The inherent complexity associated with a particular memory.

It is prudent to delineate the distinction between Memory Retrievability and Memory Retention: the former pertains to the recall probability of a singular memory, whereas the latter refers to the average recall probability across multiple memories.

Utilizing the aforementioned terms, one can define the retrievability of any given memory at time $t$ following $n$ successful revisions:

$$ R_n(t) = \exp\left[\cfrac{t\ln{0.9}}{S_n}\right] $$

By transforming $S_n$ into the inter-revision interval, this equation bridges the gap between memory algorithms and memory models:

$$ R_n(t) = \exp\left[\cfrac{t\ln{0.9}}{I_1\prod\limits_{i=2}^{n}C_i}\right] $$

Herein:

• $I_1$ denotes the interval prior to the first revision.
• $C_i$ represents the ratio between the $i$-th revision interval and the preceding $i-1$ revision interval.

The objective of memory algorithms is to accurately compute $I_1$ and $C_i$, thereby ascertaining the stability of memory across varied students, materials, and revision cycles, which facilitates the optimization of revision intervals.

To recapitulate, both SM-0 and SM-2 algorithms have an $I_i$ of one day. In SM-0, $C_i$ is a predetermined constant, whereas in SM-2, $C_i$ is a variable Ease Factor (EF) that adjusts in response to user input. It is imperative to note that each card's $C_i$ is independent of others. SM-4 endeavored to disrupt this autonomy, an innovation which continues to be refined in SM-5 and subsequent algorithms.

So the question that begs elucidation is, what is the relationship between $C_i$ and the tri-variable model of memory?

One could ponder this by examining how the state of memory updates during each review. Below are some empirical observations, corroborated by data from vocabulary learning platforms like Skritter:

• Impact on Memory Stability: A higher $S$ yields a smaller $C_i$. This signifies that as memory becomes more stable, its subsequent stabilization becomes increasingly arduous.
• Influence on Memory Retrievability: A lower $R$ results in a larger $C_i$. This implies that a lower probability of recall leads to greater post-recall stability.
• Ramifications of Memory Difficulty: A higher $D$ engenders a smaller $C_i$. Essentially, greater complexity in the material leads to a slower rate of stability enhancement.

Due to the multifarious factors at play, $C_i$ is complex to calculate. SuperMemo employs a multi-dimensional matrix to represent $C_i$ as a multivariable function and adjusts the matrix values during the user's learning journey to approximate real-world scenarios.

For the sake of subsequent discourse, we shall adopt SM-17's nomenclature for $C_i$: Stability Increase (SInc). The term implies that $C_i$ represents the multiplicative growth in memory stability before and after repetition.

Let us now delve into a more detailed exposition of Stability Increase.

Review Section

Question	Answer
Which three variables are encapsulated in the tri-variable model of memory?	Memory Stability, Memory Retrievability, and Memory Difficulty
What differentiates Memory Retrievability from Memory Retention Rate?	The former pertains to the attributes of individual memories, whereas the latter refers to the general attributes of the entire set of memories.
What two parameters serve as the linchpin connecting the tri-variable model of memory and memory algorithms?	The initial review interval $I_1$ and the ratio $C_i$ between successive intervals.
What nomenclature is applied to $C_i$?	Stability Increase

Memory Stability Increase

In this chapter, we momentarily set aside the influence of memory difficulty to focus on the intricate relationship between memory stability augmentation, stability, and retrievability.

Data for the ensuing analysis is furnished by SuperMemo users and scrutinized by Wozniak through controlled variables and linear regression techniques.

The Correlation Between Stability Increase and Memory Stability

Upon investigating the Stability Increase (SInc) matrix, it became evident that for a given level of Retrievability (R), the function of SInc with respect to Stability (S) can be aptly characterized by a negative power function.

By taking the logarithm of both Stability Augmentation (Y-axis) and Stability (X-axis), the following graphical representation is attained:

This corroborates our prior qualitative conclusion, "As S increases, $C_i$ decreases," and provides a more nuanced delineation of its functional properties.

The Interrelationship Between Stability Increase and Memory Retrievability

As predicted by the spacing effect, Stability Increase (SInc) is more pronounced when Retrievability (R) is low. After analyzing multiple datasets, it was observed that SInc demonstrates exponential growth as R diminishes—a surge that surpasses initial expectations, thereby further substantiating the spacing effect.

Upon logarithmically transforming Retrievability (X-axis), the following visual representation is achieved:

Intriguingly, SInc may fall below one when R is at 100%. Molecular-level research suggests an increase in memory instability during review sessions, thereby corroborating once more that rote repetition not only squanders time but also impairs memory.

Conclusions Drawn from the Stability Increase Function

In light of the aforementioned fundamental laws, one can derive an array of compelling conclusions through varied perspectives and combinatorial approaches.

Linear Relationship Between Stability Increase Coefficient and Interval

As time (t) increases, Retrievability (R) exponentially diminishes, while Stability Increase (SInc) conversely exhibits an exponential ascent. These two exponential behaviors counterbalance each other, yielding an approximately linear trajectory.

Expected Increase of Memory Stability

Optimization in learning encompasses diverse benchmarks; one could tailor strategies for specific retention rates or aim to maximize memory stability. In either scenario, comprehending the anticipated stability augmentation proves advantageous.

We define the expected stability augmentation as:

$$ E(SInc) = SInc \times R $$

This equation divulges a startling revelation: the apex of anticipated stability augmentation occurs when the retention rate resides between 30% and 40%.

It's crucial to note that maximal anticipated stability augmentation does not necessarily equate to the swiftest learning velocity. For the most efficacious review strategy, refer to the forthcoming SSP-MMC algorithm.

Review Section

Question	Answer
What mathematical function describes the relationship between stability augmentation and memory stability?	Negative power function
What mathematical function describes the relationship between stability augmentation and memory retrievability?	Exponential function

Memory Complexity

Memory stability during spaced repetition is contingent upon the quality of review, termed here as memory complexity. For efficacious review sessions, knowledge associations must remain simplistic—even if the knowledge itself is intricate. Flashcards can encapsulate complex knowledge architectures, yet individual flashcards ought to remain atomic.

In 2005, we formulated an equation to describe the review of composite memories. We observed that the stability of a composite memory behaves akin to resistance in a circuit; parallel resistance allows greater electrical current to pass through. (*Note: Composite is used in lieu of complex to emphasize its composed nature of simpler elements.)

Composite knowledge yields two primary ramifications:

• Augmentation in interference from additional information fragments
• Difficulty in uniformly stimulating the sub-components of the memory during review

Suppose we possess a composite flashcard that requires the memorization of two fill-in-the-blank fields. Assume both blanks are equally challenging to remember. Hence, the retrievability of the composite memory is the product of the retrievabilities of its sub-memories.

$$ R = R_a \times R_b $$

Inserting this into the decay curve equation,

$$ R = e^{ \frac{t \ln 0.9}{S_a}} \times e^{ \frac{t \ln 0.9}{S_b}} = e^{ \frac{t \ln 0.9}{S}} $$

Here, $S$ denotes the stability of this composite memory. We can deduce:

$$ \frac{t \ln 0.9}{S} = \frac{t \ln 0.9}{S_a} + \frac{t \ln 0.9}{S_b} $$

Leading to,

$$ S = \frac{S_a \times S_b}{S_a + S_b} $$

Remarkably, the stability of a composite memory will be inferior to the stabilities of its constituent memories. Based on this derivation, the stabilities of the two sub-memories will converge towards the stability of the more challenging sub-memory.

As complexity ascends beyond a certain threshold, the establishment of enduring memory stability becomes unattainable. Succinctly put, the only alternative to engraining an entire tome into one's memory is ceaseless rereading—a futile endeavor.

Review Section

Question	Answer
What is the relationship between the retrievability $R$ of a composite memory and the retrievabilities $R_a, R_b$ of its constituent memories?	$R = R_a \times R_b$; the retrievability of a composite memory is the product of the retrievabilities of its individual components.
What is the comparative magnitude between the stability $S$ of a composite memory and the stabilities $S_a, S_b$ of its constituent memories?	The stability of a composite memory is inferior to the stabilities of its individual components.
How does the stability of a composite memory change as the number of its constituent memories increases?	It progressively diminishes, asymptotically approaching zero.

Day 3: Following Latest Progresses

Having delved into various theories of memory, it is high time to put these abstract concepts into pragmatic use. We have elucidated the rudimentary principles such as $1+1=2$; now let us collectively explore this infinite series.

Brace yourselves, as what follows dispenses with review sections and takes a precipitous climb in complexity.

Build Dataset

Data serves as the lifeblood for any memory algorithm. Bereft of robust data, even the most skilled artisan would find herself constrained, akin to a cook without ingredients. The collation of pertinent, comprehensive, and precise data delineates the upper boundary of a memory algorithm's efficacy.

To capture a nuanced portrait of an individual's memory function, we must first articulate the fundamental tenets that define an act of memory. Consider, what key attributes constitute an episode of memory?

At the most elemental level, the pillars are easily discernable: who (the subject), when (the temporal context), and what (the action) forms the memory. As for the domain of memory, we can delve deeper: what precisely was memorized (the content), how well was it retained (the feedback), and what was the temporal investment (the cost), among other variables.

Taking these attributes into consideration, we can encapsulate a singular episode of memory behavior within a tuple:

$$ e := (\text{user}, \text{item}, \text{time}, \text{response}, \text{cost}) $$

For instance, the tuple:

$$ e := (\text{Jarrett}, \text{apple}, \text{2022-04-01 12:00:01}, \text{Forgotten}, \text{5s}) $$

Serves to illustrate that Jarrett endeavored to memorize the word 'apple' at 12:00:01 on April 1, 2022, but regrettably, the endeavor concluded in forgetfulness after a temporal investment of 5 seconds.

Armed with this foundational construct of a memory behavior event, we can extrapolate a plethora of additional salient information.

For example, in the context of spaced repetition, the interval between successive repetitions is of paramount importance. Utilizing the aforementioned tuple, one can collate the events by 'user' and 'item,' sequentially sort them by 'time,' and subsequently derive the interval by subtracting adjacent timestamps. Although this approach incurs a degree of storage redundancy, it mitigates computational overhead.

Beyond temporal intervals, both the historical sequences of 'responses' and 'intervals' represent crucial attributes. Sequences such as "Forgotten, Remembered, Remembered, Remembered" or "1 day, 3 days, 6 days, 10 days," offer a comprehensive reflection of an individual memory episode's longitudinal history and can also be incorporated directly into the event tuple:

$$ e_{i} := (\text{user}, \text{item}, \boldsymbol{\Delta t_{1:i-1}}, \boldsymbol{r_{1:i-1}}, \Delta t_i, r_i) $$

For those intrigued by the data, you may download the open-source dataset of the MaiMemo vocabulary app here for your own analysis.

The DSR Model

With data at our disposal, how might we harness it effectively? Revisiting the tri-variable memory model elucidated on Day 2, we are primarily interested in discerning the various attributes of a memory state, which are conspicuously absent from the data we've presently aggregated. Consequently, our objective in this section is to delineate how raw memory data can be transmuted into discernible memory states and the corresponding state transition matrices.

Memory States

The acronym DSR delineates the tripartite elements of Difficulty, Stability, and Retrievability. Let us commence by focusing on Retrievability, which signifies the probability of successful recall at a given temporal juncture. However, the memory behavior events we've been recording are inherently post-recall outcomes. In the parlance of probability theory, each memory behavior is a singular Bernoulli trial with only two possible outcomes—success or failure—the probability of which equates to its Retrievability.

Hence, to precisely gauge Retrievability, the most straightforward methodology one might conceive of would be to subject a particular memory to an infinite array of independent trials, subsequently tallying the frequency of successful recalls. However, this approach is fundamentally infeasible in practical terms, as subjecting a memory to repeated trials alters its inherent state. We cannot act as mere passive observers; we inevitably induce perturbations in the memory state during measurement. (Note: Given the current state of neuroscience, we lack the capability to measure memory states at the neuronal level, rendering this approach currently unfeasible.)

Are we, then, utterly incapacitated in our endeavors? There are, at present, two compromise methodologies for measurement: (1) Disregarding material-specific variances—both SuperMemo and Anki fall into this category; (2) Overlooking individual learner differences—MaiMemo exemplifies this approach. (Note: While these considerations are presently being integrated, they were initially absent when penning this passage, but such omissions should not impair the comprehension of the ensuing discourse.)

Overlooking the idiosyncrasies of individual memory items means that when measuring Retrievability, one collates data that is identical in every attribute except for the memory item itself. While it is impractical to conduct multiple independent trials for a single learner and a single item, trials involving multiple items for one learner become viable. Conversely, ignoring learner-specific differences entails statistical analysis across multiple learners for a single item.

Given the voluminous data set afforded by MaiMemo, this section exclusively focuses on measurement methodologies that eschew learner variability. Once this factor is discounted, we are enabled to aggregate a newly refined ensemble of memory behavior events:

$$ e_{i} := (item, \boldsymbol{\Delta t_{1:i-1}}, \boldsymbol{r_{1:i-1}}, \Delta t_i, p_i, N) $$

Herein, $N$ represents the number of learners with identical historical behaviors regarding the memory item in question. The Retrievability $p = \frac{n_{r=1}}{N}$ signifies the ratio of learners who have successfully recalled the item. When $N$ is sufficiently large, the ratio $\frac{n_{r=1}}{N}$ approximates true Retrievability.

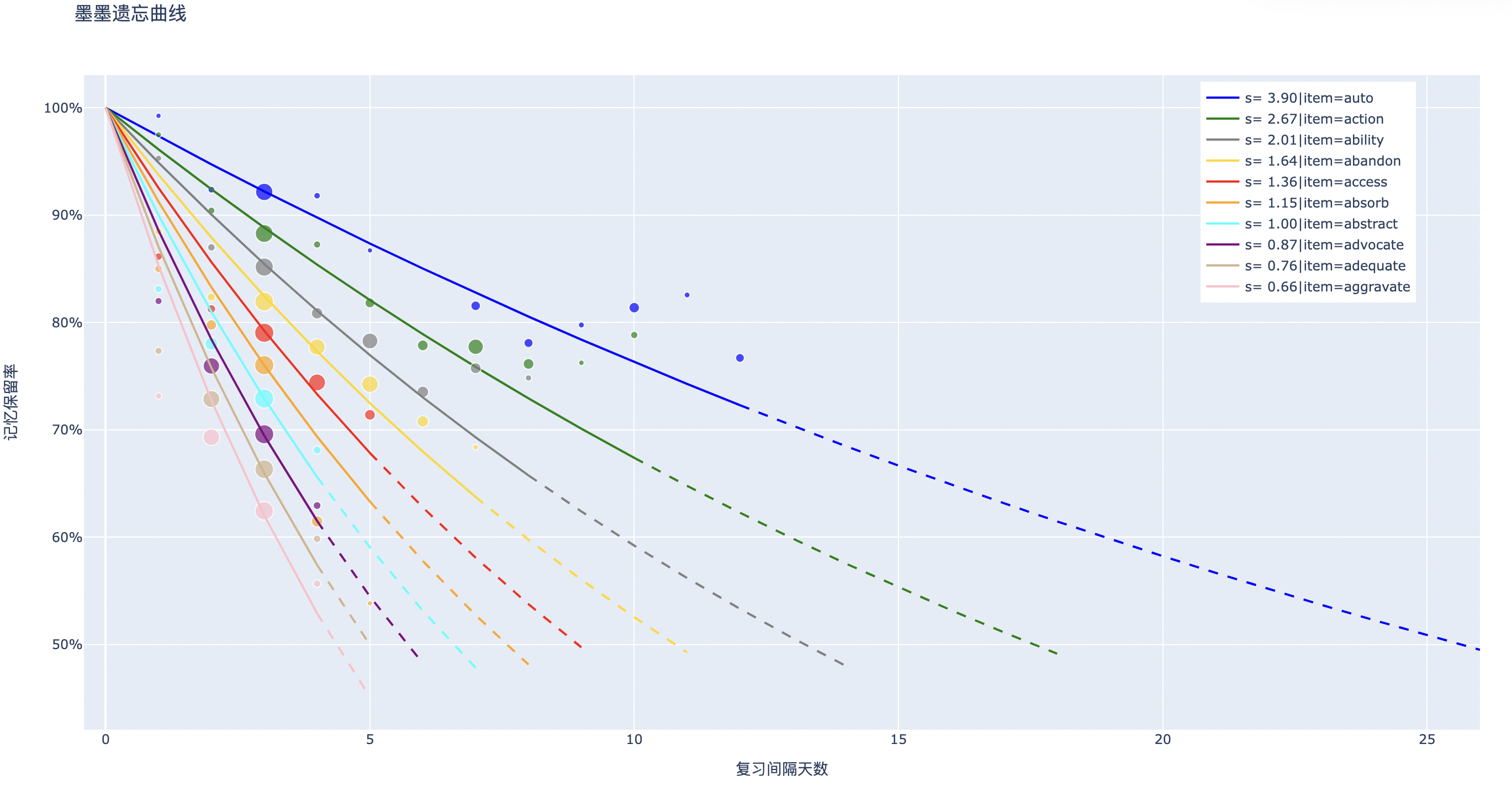
With Retrievability duly accounted for, the conundrum of Stability is correspondingly solved with relative ease. The method for measuring Stability is the Forgetting Curve. Utilizing the collected data, an exponential function can be employed for regression analysis to compute the Stability of memory behavior events with identical $(item, \boldsymbol{\Delta t_{1:i-1}}, \boldsymbol{r_{1:i-1}})$ attributes.

The scatter plot points within the graph have coordinates $(\Delta t_i , p_i)$, with their relative sizes proportional to $\log N$. The curve represents the fitted Forgetting Curve.

Lastly, the concept of difficulty merits our attention. How can one discern the level of difficulty from the gathered memory data? Let us commence with a rudimentary thought experiment. Suppose a cohort of learners is exposed for the first time to the words "apple" and "accelerate." How might one utilize memory behavior data to distinguish the relative difficulty of these two terms?

The most straightforward approach would be to administer an immediate test on the subsequent day, collate the memory behavior data, and statistically analyze which word boasts a higher rate of successful recollection. From this foundational observation, one could extrapolate that the Stability observed after the initial memorization event serves as a reliable indicator of difficulty.

However, there is no universally agreed-upon standard for utilizing post-initial-memorization Stability to delineate varying degrees of difficulty. Furthermore, no definitive conclusion has been reached as to which method of classification is most efficacious. Given the introductory nature of this text, a detailed exposition on the topic shall be eschewed.

State Transition

Hitherto, we have been equipped to transform memory data into discernible memory states, denoted as $(D_i, S_i, R_i)$.

Our subsequent endeavor involves delineating the transitional relationships between these states. Specifically, if a review of the state $(D_i, S_i, R_i)$ occurs after a temporal interval $\Delta t$, resulting in a recollection outcome of $r$, a new memory state $(D_{i+1}, S_{i+1}, R_{i+1})$ is engendered. What, then, is the relational nexus among $(D_{i+1}, S_{i+1}, R_{i+1})$, $(D_i, S_i, R_i)$, $\Delta t$, and $r$?

Initially, the data encapsulating these memory states must be meticulously organized to facilitate analytical scrutiny, denoted as $(D_i, S_i, R_i, \Delta t, r, D_{i+1}, S_{i+1}, R_{i+1})$.

It should be noted that $R_{i+1}$ will invariably ascend to 100% immediately post-review, thus rendering it extraneous in the analytical process. Similarly, one can ascertain either $S_i$ or $\Delta t$ if $R_i$ is known, thereby making $\Delta t$ superfluous.

Ultimately, the state transition data requiring analysis is represented as $(D_i, S_i, R_i, r, D_{i+1}, S_{i+1})$.

In this context, the stability increment $\frac{S_{i+1}}{S_i} = SInc$ can be elucidated through certain axioms propounded in the chapter on memory stability growth, such as:

$$ SInc = a S^{-b} $$

$$ SInc = c e^{-d R} $$

From the aforementioned formulae, where the impact of difficulty $D$ has been judiciously omitted for the purpose of this analysis, we can extrapolate the following equation for instances of successful recollection ($r = 1$):

$$ S_{i+1} = S_{i} \cdot a S_{i}^{-b} e^{-c R_i} $$

Based on this equation, we are empowered to prognosticate the learner's memory state $(D_{i+1}, S_{i+1})$ subsequent to each successful recollection. Analogously, instances of failed recall can be characterized by a disparate set of state transition equations.

Spaced Repetition System Simulation

Armed with the DSR (Difficulty, Stability, Recallability) memory model, we are poised to simulate memory retention under an array of review strategies. How, precisely, can we construct such a simulation? Our point of departure must be an empirical understanding of how the average individual utilizes spaced repetition software.

Consider the hypothetical scenario where Xiao Ye endeavors to prepare for a graduate entrance English examination four months hence, employing spaced repetition techniques to commit the test's vocabulary to memory while simultaneously allocating time for other subjects.

In this construct, two salient constraints manifest: the length of the learning cycle in days and the daily allotment of study time. A Spaced Repetition System (SRS) simulator must incorporate both these parameters, thus bifurcating the simulation along two dimensions—diurnal (by day) and intraday (within the day). Moreover, the vocabulary set dictated by the examination syllabus is finite; hence, the SRS simulation includes a bounded set of flashcards from which the learner selects material for daily study and review. The sequencing of these review tasks is orchestrated by a spaced repetition scheduling algorithm. In summary, an SRS simulation necessitates:

1. A corpus of study material
2. A model learner
3. A scheduling algorithm
4. A specified simulation duration (both diurnal and intraday)

The learner's behavior can be modeled via the DSR framework, offering feedback and memory states following each review. The scheduler may deploy algorithms like the SM-2 algorithm, the Leitner box system, or incrementally increasing interval tables, among other interval scheduling techniques. The simulation's duration and material set must be tailored to suit the scenario one wishes to model.

To operationalize the simulation, we proceed by elucidating its two dimensions. Evidently, the simulation ought to unfold in a temporally sequential manner, progressing day-by-day into the future. Each simulated day comprises the learner's interactions with individual flashcards. Thus, an SRS simulation can be conceptualized as consisting of two nested loops: the outer loop signifying the current simulated date, and the inner loop representing the current flashcard under review. Within this internal loop, time expenditure for each review is stipulated; when cumulative time exceeds the daily study cap, the loop is automatically exited in preparation for the ensuing day's tasks.

Here is the pseudocode for SRS Simulation:

The pertinent Python code has been open-sourced on GitHub for readers who are intrigued enough to delve into the source code: L-M-Sherlock/space_repetition_simulators: Spaced Repetition Simulators (github.com)

SSP-MMC Algorithm

Having delineated both the DSR model and SRS simulations, we are well-equipped to forecast a learner's mnemonic state and memory retention under predefined review schedules. Nevertheless, we have yet to address the quintessential question: What constitutes the most efficacious review schedule? How does one ascertain the optimal study regimen? The SSP-MMC algorithm addresses this conundrum from the perspective of optimal control theory.

SSP-MMC is an acronym for Stochastic Shortest Path and Minimize Memorization Cost, encapsulating both the mathematical toolkit and the optimization objective underpinning the algorithm. The ensuing discourse is adapted from my graduate thesis, "Research on Review Scheduling Algorithms Based on LSTM and Spaced Repetition Models," and the conference paper A Stochastic Shortest Path Algorithm for Optimizing Spaced Repetition Scheduling.

Problem Setup

The objective of spaced repetition methodologies lies in aiding learners to efficiently cultivate enduring memories. Memory stability, thus, serves as an index for the robustness of long-term retention, while the frequency of reviews and the time expended during each session encapsulate the cost of memory. Consequently, the aim of optimizing spaced repetition scheduling can be articulated as follows: Within a given framework of memorization cost constraints, the goal is to enable as much learning material as possible to achieve a predetermined level of memory stability, or alternatively, to attain this level of stability for a specific body of material at the lowest possible cost. The latter challenge can be distilled down to the minimization of memorization cost (MMC).

Conforming to the Markovian nature, the DSR model posits that the status of each memory instance is influenced solely by its preceding status and the contemporaneous input and outcome of a review. The result of the recall follows a stochastic distribution that is correlated with the review interval. Given the stochastic nature of memory-state transitions, the number of reviews required for a piece of memory material to attain the target stability remains indeterminate. As such, the task of spaced repetition scheduling can be conceptualized as an infinite-horizon stochastic dynamic programming problem. Given that the optimization objective is to elevate memory stability to a pre-defined criterion, the problem converges to a terminal state and can thus be recast as a Stochastic Shortest Path (SSP) problem.

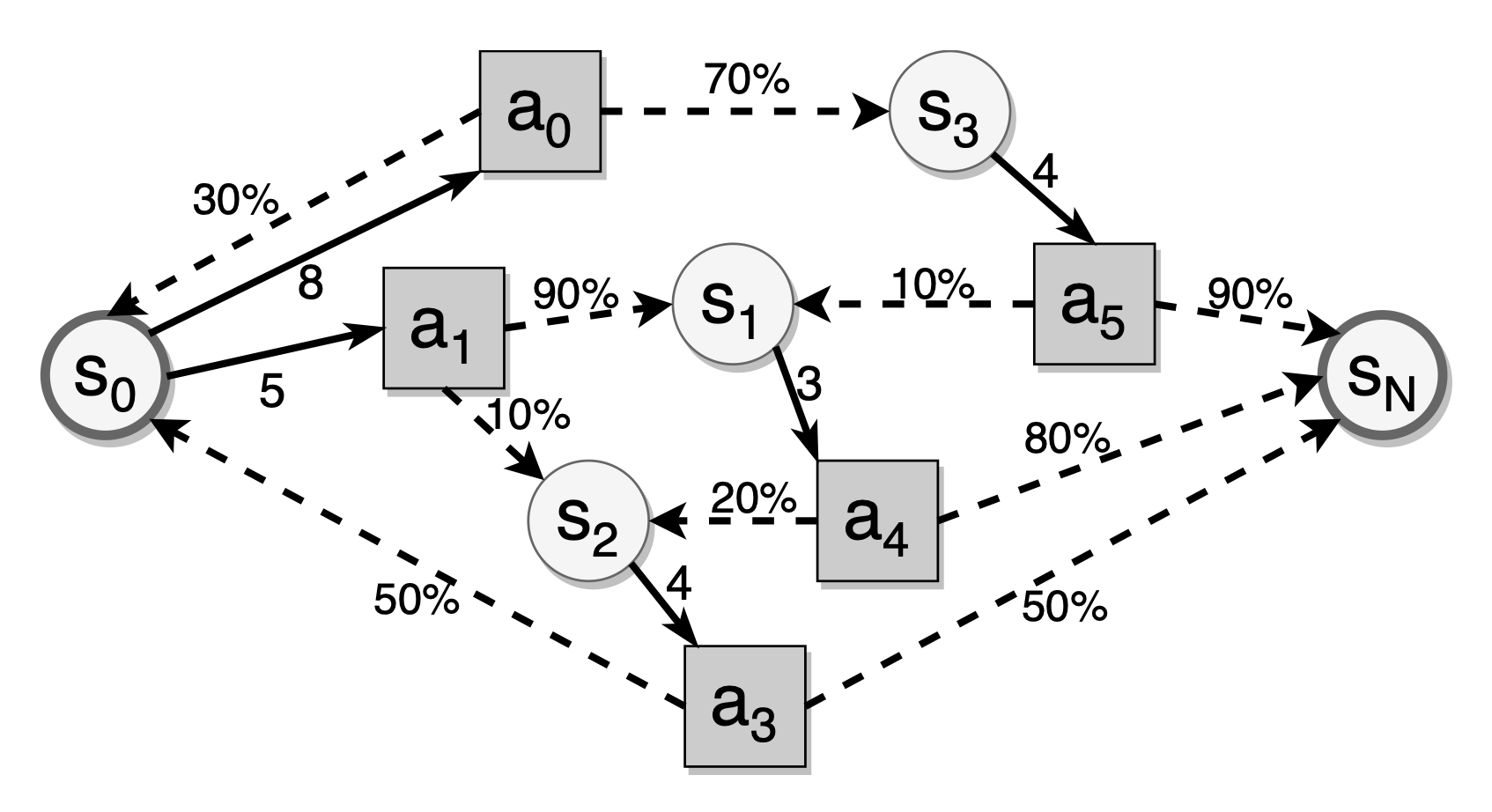
As illustrated in the figure above, circles represent memory states while squares symbolize review actions—specifically, the intervals following the current review. Dashed arrows signify state transitions contingent on a given review interval, whereas solid edges depict the available review intervals within a given memory state. Within the realm of spaced repetition, the Stochastic Shortest Path problem is concerned with identifying the optimal review interval to minimize the expected cost incurred in reaching the target state.

Formulation

To address this quandary, one can employ a Markov Decision Process (MDP) to model the review process for each flashcard, incorporating a set of states $\mathcal{S}$, actions $\mathcal{A}$, state transition probabilities $\mathcal{P}$, and a cost function $\mathcal{J}$. The aim of the algorithm is to identify a policy $\pi$ that minimizes the anticipated review cost for reaching the target state $s_N$.

$$ \pi^* = \underset{\pi \in \Pi}{\text{argmin}} \lim_{{N \to \infty}} \mathbb{E}{s{0}, a_{0}, \ldots} \left[ \sum_{t=0}^{N} \mathcal{J}(s_{t}, a_{t}) \mid \pi \right] $$

The state space $S$ is contingent upon the dimensions of the memory model. In the DSR framework, there are merely two state variables, thus the state can be denoted as $ s = (D, S) $. The action space $\mathcal{A} = {\Delta t_1, \Delta t_2, \ldots, \Delta t_n }$ comprises $N$ intervals at which reviews can be scheduled. The state transition probability $\mathcal{P}_{s,a}(s')$ represents the likelihood of a flashcard being recalled under state $s$ and action $a$. The cost function $\mathcal{J}$ is defined as:

$$ \begin{aligned} \mathcal{J}(s_0) &= \lim_{{N \to \infty}} \mathbb{E} \left[ \sum_{{t=0}}^{N-1} g_t(s_t, a_t(s_t), r_t) \right] \\ r_t &\sim \text{Bernoulli}(p_t) \end{aligned} $$

Here, $g_t$ denotes the cost incurred during each review, while $r_t$ is the recall outcome, following a Bernoulli distribution. The target state $s_N$ corresponds to the desired level of memory stability.

Algorithm

To resolve the Markov Decision Process $\text{MDP}(\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{J})$, one can leverage the Value Iteration method. The Bellman equation governing this method is expressed as:

$$ \begin{aligned} \mathcal{J}^(s) &= \min_{a \in \mathcal{A}(s)} \left[ \sum_{s'} \mathcal{P}_{s,a}(s') \left( g(r) + \mathcal{J}^(s') \right) \right] \ s' &= \mathcal{F}(s,a,r,p) \end{aligned} $$

Here, $\mathcal{J}^*$ signifies the optimal cost function, and $\mathcal{F}$ represents the state transition function, specifically within the context of the DSR model. For the sake of simplicity, the cost incurred during each review—affected solely by the outcome of recall—is delineated as: $g(r) = a \cdot r + b \cdot (1-r)$, where $a$ is the cost of successful recall and $b$ is the cost of failed recall.

In accordance with this Bellman equation, the Value Iteration algorithm employs a cost matrix to chronicle optimal costs and a policy matrix to retain the most favorable action for each state, as depicted in the following diagram.

The algorithm perpetually iterates through each available review interval for every memory state, contrasting the expected memory cost of the current review interval with the cost stored in the cost matrix. Should the current interval manifest a lower cost, the corresponding entries in both the cost and policy matrices are updated, eventually converging to the optimal intervals and costs for all memory states.

Thus, by amalgamating this optimal review strategy with the DSR model for predicting memory states, an efficacious review schedule can be orchestrated for each learner employing the SSP-MMC memory algorithm.

This algorithm has been open-sourced in MaiMemo's GitHub repository: maimemo/SSP-MMC: A Stochastic Shortest Path Algorithm for Optimizing Spaced Repetition Scheduling (github.com). Readers interested in an in-depth examination are encouraged to fork a copy for local exploration.

Conclusion

Congratulations on reaching the end! Should you not yet be six feet under, you have successfully gained an introductory understanding of spaced repetition memory algorithms!

You may still harbor myriad questions—some of which may already have answers, while many undoubtedly pertain to as-yet unexplored terrains.

My capacity to address these questions is decidedly limited, yet I am committed to dedicating a lifetime to advancing the frontiers of spaced repetition algorithms.

With this in mind, I extend an invitation to join me in unraveling the enigma of memory. Will you be willing to accompany me on this intellectual odyssey?

---

Original link: https://l-m-sherlock.github.io/thoughts-memo/post/srs_algorithm_introduction/