-
-
Notifications
You must be signed in to change notification settings - Fork 139
Spaced Repetition Algorithm: A Three‐Day Journey from Novice to Expert
I am Jarrett Ye, the principal author of the paper A Stochastic Shortest Path Algorithm for Optimizing Spaced Repetition Scheduling and the paper Optimizing Spaced Repetition Schedule by Capturing the Dynamics of Memory. I currently serve at MaiMemo Inc., where I am chiefly responsible for developing the spaced repetition algorithm within MaiMemo's language learning app. For a detailed account of my academic journey leading to the publication of these papers, please refer to: How did I publish a paper in ACMKDD as an undergraduate?
This tutorial, "Spaced Repetition Algorithms: A Three-Day Journey from Novice to Expert," is adapted from the manuscript I initially prepared for internal presentations at MaiMemo. The objective is to elucidate what exactly spaced repetition algorithms are investigating and to inspire new researchers to contribute to this field and advance the progress of learning technology. Without further ado, let us embark on this intellectual journey.
Since our school days, most students have had two simple intuitions:
- Reviewing information multiple times helps us remember it better.
- Different memories fade at different rates, not all at once.
These insights raise further questions:
- How much knowledge have we already forgotten?
- How quickly are we forgetting them?
- What is the best way to schedule reviews to minimize forgetting?
In the past, few people have measured these factors or used them to optimize their review schedules. The focus of spaced repetition algorithms is to understand and predict how we remember things and to schedule our reviews accordingly.
In the next three days, we will delve into spaced repetition algorithms from three perspectives:
- Empirical Algorithms
- Theoretical Models
- Latest progress
Today we begin our journey by diving into the simplest yet impactful empirical algorithms. We'll uncover the details and the ideas that guide them. But first, let's trace the roots of a term that pervades this field — spaced repetition.
For readers new to the subject of spaced repetition, let's learn about the concept of the "forgetting curve."

After we first learn something, whether it's from a book or a class, we start to forget it. This happens gradually, just like the forgetting curve that slopes downward.
The forgetting curve provides an illustration of the way our memory retains knowledge. It exhibits a unique trajectory: in the absence of active review, the decay of memory is initially swift and slows down over time.
How can we counteract this natural propensity to forget? Let's consider the power of reviews.

Introducing periodic reviews results in a flattened forgetting curve, indicating a slower decay of memory over time.
When we review information and update the forgetting curve, we find that the curve has become flatter. This indicates that the rate at which we forget has slowed down.
So how should one optimize these review intervals for enhanced memory retention?

Notice the varying lengths of the review intervals? Shorter intervals are used for unfamiliar content, while longer ones are employed for more familiar material, which scatters reviews over different timings in the future. This tactic, known as spaced repetition, augments long-term memory retention.
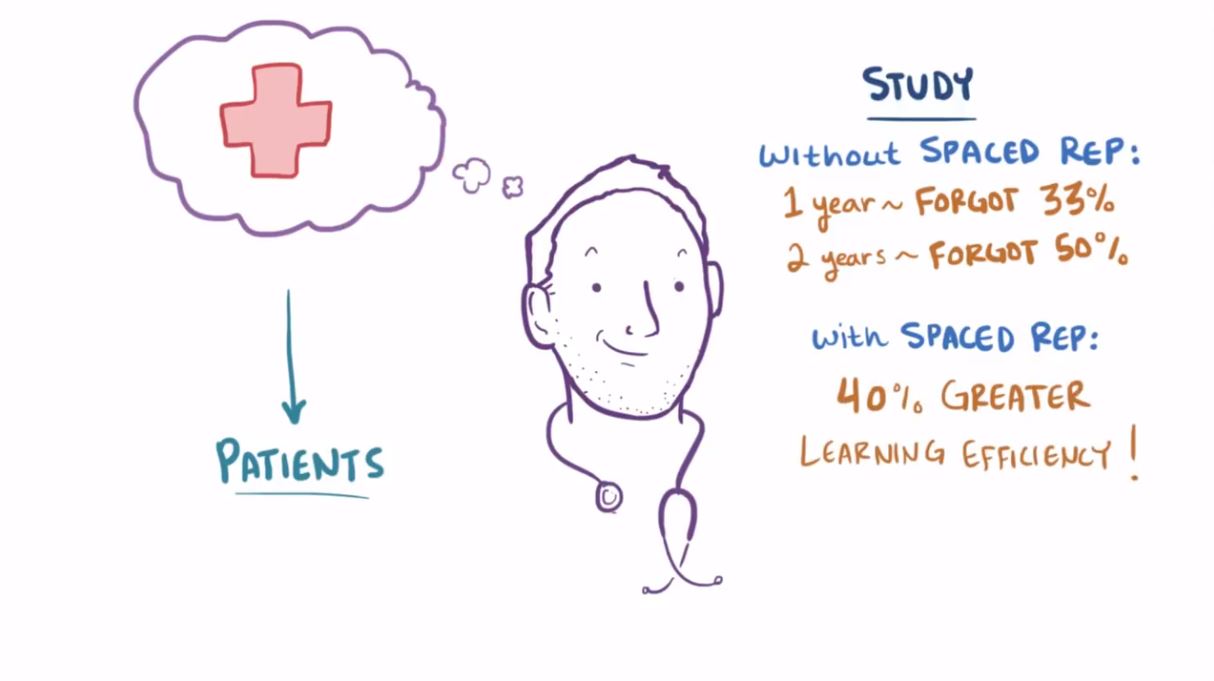
But how effective is it? Let's examine some stats from medical students.
If spaced repetition is so impactful, why hasn't it gained mass adoption?
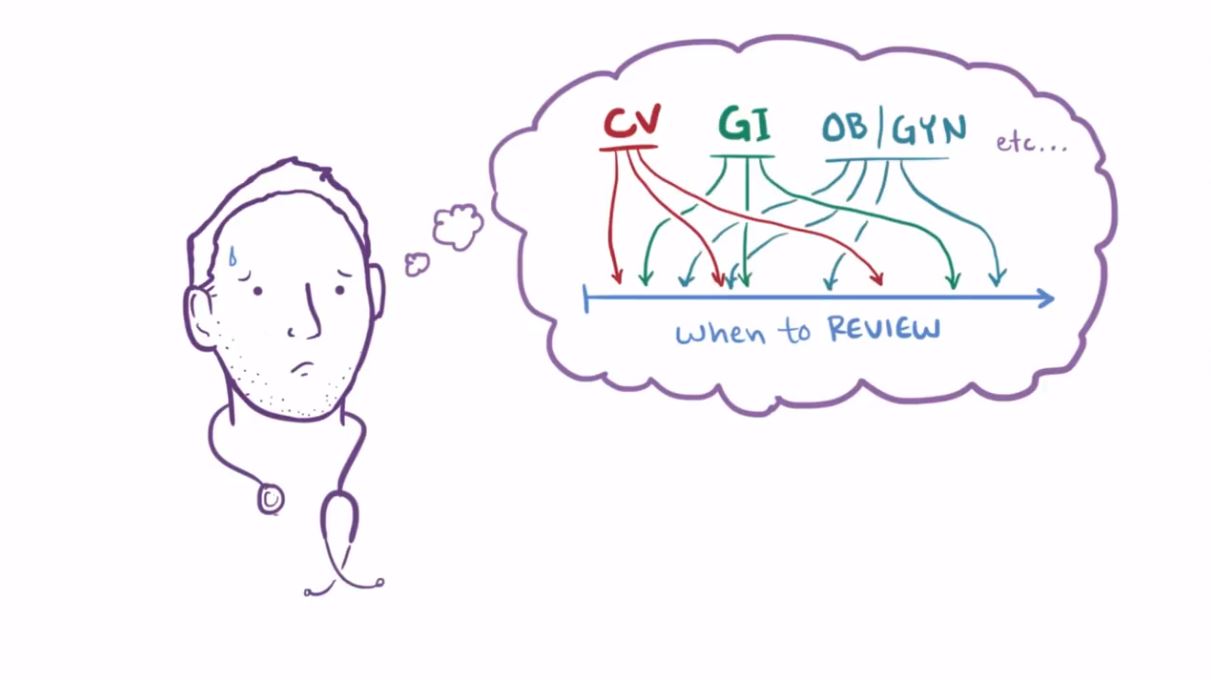
The obstacle lies in the overwhelming volume of knowledge to learn. Each piece of knowledge has its own unique forgetting curve, making manual tracking and scheduling an impossible mission.
This introduces the role of spaced repetition algorithms: automating the tracking of memory states and arranging efficient review schedules.
By now, you should have a basic understanding of spaced repetition. But questions likely still linger, such as optimal review timing and best practices for efficient spaced repetition. The answers to these questions await in the coming chapters.
| Question | Answer |
|---|---|
| What aspect of memory does the forgetting curve capture? | The curve describes how knowledge retention decays over time in our memory. |
| How does memory retention decline when we don't review information? | It decreases swiftly initially and then slows down. |
| After a successful review, what distinguishes the new forgetting curve from its predecessor? | The new curve is flatter, indicating a slower rate of forgetting. |
| How does spaced repetition accommodate content of different familiarity levels? | Shorter intervals are applied for unfamiliar content, while longer ones are set for familiar material. |
| What function do algorithms serve in spaced repetition? | They automate the tracking of memory states and the arrangement of efficient review schedules. |
Having delved into the concept of spaced repetition, you may find yourself pondering this guiding principle:
Shorter intervals are used for unfamiliar content, while longer ones are employed for more familiar material, which scatter reviews over different timings in the future.
What exactly defines these 'short' or 'long' intervals? Furthermore, how can one distinguish between material that is 'familiar' and that which is 'unfamiliar'?
Intuitively, the slower the material is forgotten in our memory, the more familiar it is. And a reasonable interval should minimize our forgetting. But the less we want to forget, the shorter the interval should be. The shorter the interval, the higher the frequency of reviews.
It seems there's an inherent contradiction between the frequency of reviews and the rate of forgetting — how to reconcile this discrepancy?
If you were to resolve this conflict, what would you need to continue to learn? What kind of experiment would you design? Keep thinking about them, and even better, write them down!
Let's take a look at how the creator of the first computational spaced repetition algorithm set out on his journey in the exploration of memory.
In 1985, a young college student named Piotr Woźniak (aka Woz) was struggling with the problem of forgetting:
The above image shows a page from his vocabulary notebook, which contained 2,794 words spread across 79 pages. Each page had about 40 pairs of English-Polish words. Managing all those reviews was a headache for Woz. At first, he didn't have a systematic plan for reviewing the words; he just reviewed whatever he had time for. But he did something crucial: he kept track of when he reviewed and how many words he forgot, allowing him to measure his progress.
He compiled a year's worth of review data and discovered that his rate of forgetting ranged between 40% and 60%. This was unacceptable to him. He needed a reasonable study schedule that would lower his forgetting rate without overwhelming him with reviews. To find an optimal review interval, he commenced his own memory experiments.
Woz wanted to find the longest possible time between reviews while keeping the forgetting rate under 5%.
Here are the details about his experiment:
Materials: Five pages of English-Polish vocabulary, each with 40 word pairs.
Initial Learning: Memorize all 5 pages of material. Look at the English word, recall the Polish translation, and then check whether the answer is correct. If the answer is correct, eliminate the word pair from this phase. If the answer if incorrect, try to recall it later. Kepp doing this until all the answers are correct.
Initial Review: A one-day interval was employed for the first review, based on Woz's previous review experience.
The ensuing key phases —A, B, and C— revealed the following:
Phase A: Woz reviewed five pages of notes at intervals of 2, 4, 6, 8, and 10 days. The resulting forgetting rates were 0%, 0%, 0%, 1%, and 17%, respectively. He determined that a 7-day interval was optimal for the second review.
Phase B: A new set of five pages was reviewed after 1 day for the first time and then after 7 days for the second time. For the third review, the intervals were 6, 8, 11, 13, and 16 days, with forgetting rates of 3%, 0%, 0%, 0%, and 1%. Wozniak selected a 16-day interval for the third review.
Phase C: Another fresh set of five pages was reviewed at 1, 7, and 16-day intervals for the first three reviews. For the fourth review, the intervals were 20, 24, 28, 33, and 38 days, with forgetting rates of 0%, 3%, 5%, 3%, and 0%. Wozniak opted for a 35-day interval for the fourth review.
Subsequently, Woz conducted experiments to identify the optimal interval for the fifth review. However, the time required for each successive phase was approximately double that of the preceding one. Ultimately, he formalized the SM-0 algorithm on paper.
- I(1) = 1 day
- I(2) = 7 days
- I(3) = 16 days
- I(4) = 35 days
- for i>4: I(i) = I(i-1) * 2
- Words forgotten in the first four reviews were moved to a new page and cycled back into repetition along with new materials.
In this context,
The goal of the SM-0 algorithm was clear: to extend the review interval as much as possible while minimizing the rate of memory decay. Its limitations were evident as well, namely its inability to track memory retention at a granular level.
Nonetheless, the significance of the SM-0 algorithm was far-reaching. With the acquisition of his first computer in 1986, Woz simulated the model and drew two key conclusions:
- Total knowledge retention could increase over time.
- The learning rate remained relatively stable in the long term.
These insights proved that the algorithm could reconcile the tension between memory retention and the frequency of review. Woz realized that spaced repetition didn't have to drown learners in an endless sea of reviews, thereby inspiring him to continue refining spaced repetition algorithms.
| Questions | Answers |
|---|---|
| Which two factors did Woz consider for determining optimal review intervals? | Interval duration, which is linked to the frequency of review, and the rate of memory decay, associated with memory retention. |
| Why did Woz use new materials each time he sought to establish a new review interval in his experiments? | To ensure uniformity in the intervals of prior reviews, thus controlling for variables. |
| What is the primary limitation of the SM-0 Algorithm? | It uses a page of notes as the unit for review, making it unsuitable for tracking memory retention at a more granular level. |
Though the SM-0 algorithm displayed efficacy, several issues prompted Wozniak to seek refinements:
-
If a word is forgotten during the first review (after 1 day), it will be easier to forget it again during the second and third reviews (after 7 and 16 days) compared to words that were not forgotten before.
-
Pages of new notes made up of words forgotten after the fourth review have a higher chance of being forgotten even when the review schedule was the same.
The first finding made him realize that reviewing doesn't always make him more familiar with the material. Forgotten material gets even more unfamiliar, and the speed of forgetting doesn't slow down. If he keeps reviewing these words with longer gaps like the rest on the same note page, it won't work well.
The second finding made him see that not all material is equally hard. Different difficulty levels should have different review gaps.
Consequently, in 1987, armed with his initial personal computer, Woz utilized his two-year record and insights from the SM-0 algorithm to craft the SM-2 algorithm.
The details about SM-2:
- Break down the information you want to remember into small question-answer pairs.
- Use the following intervals (in days) to review each question-answer pair:
-
$I(1) = 1$ -
$I(2) = 6$ -
For
$n > 2$ ,$I(n) = I(n-1) \times EF$ -
$EF$ —the Ease Factor, with an initial value of 2.5 - After each review,
$\text{newEF} = EF + (0.1 - (5-q) \times (0.08 + (5-q) \times 0.02))$ -
$\text{newEF}$ —the post-review updated value of the Ease Factor -
$q$ —the quality grades of review, ranging from 0 - 5. If it's >= 3, it means the learner remembered, and if it's < 3, the learner forgot.
-
-
-
If the learner forgets, the interval for the question-answer pair will be reset to
$I(1)$ with the the same EF.
-
The SM-2 algorithm adds the review feedback to how often you review the question-answer pairs. The lower the EF, the smaller the interval multiplier factor; in other words, the slower the intervals grow.
The SM-2 algorithm still relies on Woz's own experimental data, but two main advantages make it a popular spaced repetition algorithm today:
-
It breaks material down into small question-answer pairs. This lets the review schedule be super specific to each pair and separates out the hard and easy material sooner.
-
It uses an "Ease Factor" and grades. So, the algorithm can modify the learner's future reviews based on how well the learn remembers the material.
Later Woz developed more empirical algorithms, such as SM-4, but I won't discuss them here.
| Questions | Answers |
|---|---|
| Why shouldn't we set a longer interval for material we forgot during a review? | The speed of forgetting doesn't slow down for that material; in other words, the forgetting curve doesn't get flatter. |
| What shows that some material is harder to remember than others? | The pages with material that was forgotten had a higher chance of being forgotten again. |
| What is the practical purpose of incorporating an "Ease Factor" and grades into the SM-2 algorithm? | This enables the algorithm to dynamically adjust future review intervals based on user performance. |
| What are the advantages of breaking material down into smaller parts for review? | It lets the algorithm separate the easiy material from the harder material sooner. |
The primary objective of SM-4 is to address the shortcomings in adaptability found within its predecessor, the SM-2 algorithm. While SM-2 has the capacity to tune review schedules for individual flashcards based on ease factors and recall grades, these adjustments are made in isolation, without regard to prior alterations made to other cards.
In other words, each flashcard is treated as an independent entity in SM-2, leaving the algorithm perpetually uninformed about the user's overall learning process, regardless of the quantity of cards reviewed. To overcome this, SM-4 introduces an Optimal Interval Matrix, replacing the existing formulae used for interval calculations:
The matrix above is called the Optimal Interval (OI) matrix. It has rows for how easy stuff is and columns for how many times you've seen it. It starts the same as SM-2, using the same formulas to decide how long to wait before looking at a card again.
To make new cards learn from what happened with old cards, the OI matrix keeps changing as the learner reviews. The main idea is: if the OI matrix says to wait X days and the learner actually waits X+Y days and still remembers with a high grade, then the OI value should be changed to something between X and X+Y.
The reason for this is simple: if the learner can remember something after waiting X+Y days and get a good score, then the old OI value was probably too short. Why not make it longer?
This naive idea allows SM-4 to be the first algorithm capable of making holistic adjustments based on the learner's experience. But, it didn't work as well as hoped. The reasons are simple:
- Each review only changes one entry of the matrix, so it takes too long to really make the OI matrix better.
- For longer review interval, it takes a long time to make them stable.
To address these issues, the SM-5 algorithm was designed. But I won't go into details here because of space limits.
| Question | Answer |
|---|---|
| What accounts for the limited adaptability of SM-2? | Adjustments are made to each flashcard in isolation, precluding the sharing of experiential insights. |
| What components does SM-4 introduce to enhance adaptability? | Optimal Interval Matrix and dynamic interval-adjustment rules. |
| What is the underlying principle for interval adjustments in SM-4? | If the learner exhibits proficient recall over extended intervals, the original interval should be longer, and vice versa. |
First discovered in 1885, the forgetting curve shows how we remember and forget. Fast-forward to 1985, when the first computer algorithm for spaced repetition aimed at finding the optimal review schedule was developed. This section has outlined the developmental progression of empirically based algorithms:
- SM-0 gathered experimental data to determine the best review intervals for a given individual and a specific type of material (Woz defined what "best" means here).
- SM-2 digitalized the algorithm for computer applications, introducing a more granular card level and incorporating adaptive ease factors and recall grades.
- SM-4 further enhanced the adaptability of the algorithm for a diverse range of learners, introducing the Optimal Interval Matrix along with rules for adjusting the intervals.
While empirical algorithms offer a valuable lens through which to understand spaced repetition, it's really hard to make it better without a systematic theoretical underpinning. We're diving into the theory part next!
Spaced repetition algorithms sound like a theoretical study, but I've spent a lot of time discussing empirical algorithms. Why?
Because Without the foundational support of empirical evidence, any theoretical discourse would be without merit. The gut feelings we have about how human memory works may not be accurate. So, the theories we'll discuss next will also start from what we've learned so far to ensure that they are grounded in reality.
Here's a question to think about: What factors would you consider when describing the state of something in your memory?
Before Robert A. Bjork, many researchers used memory strength to talk about how well people remembered something.
Let's revisit the forgetting curve for a moment:

First and foremost, memory retention (recall probability) clearly emerges as a pivotal variable in characterizing the state of one's memory. Derived from our everyday experiences, forgetting often manifests as a stochastic phenomenon. No one can unequivocally assert that a word memorized today will be retained ten days hence or forgotten twenty days later.
Is recall probability sufficient for description? Imagine drawing a horizontal line across these forgetting curves; each curve will intersect at a point with identical recall probabilities. Have you noticed that recall probability alone seems insufficient for differentiating the conditions at these intersections?
Relying solely on recall probability does not allow us to distinguish the rate of forgetting associated with different materials. While this rate should certainly be factored into the description of memory states, it's a variable that changes with time. Can we depict it through a time-independent metric?
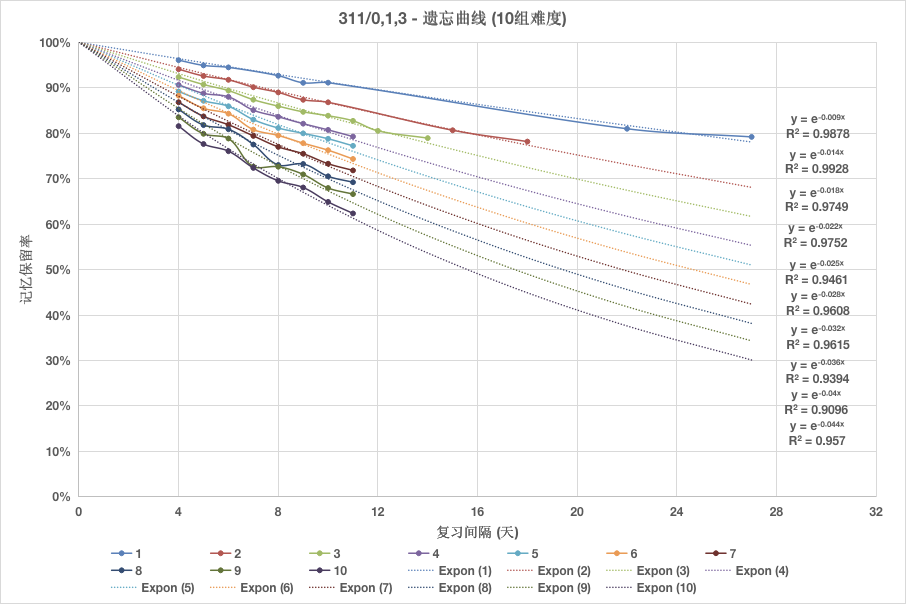
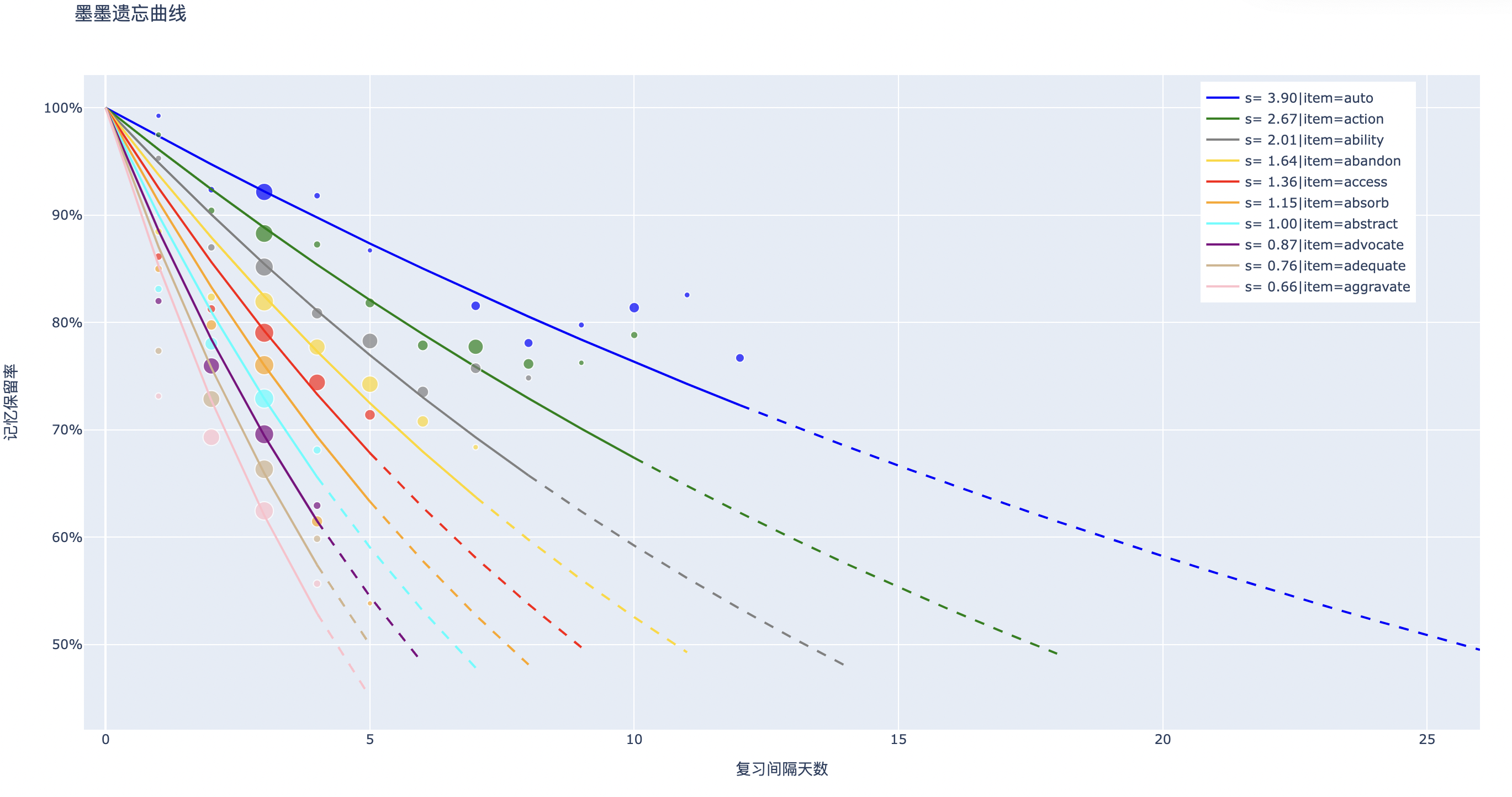
To address this problem, we must delve into the mathematical properties of the forgetting curve — a task that necessitates the gathering of extensive data to plot the curve. The data, in this tutorial, is sourced from an open dataset created from language learning application MaiMemo.
From the figure above, we find that the forgetting curve can be approximated by a negative exponential function. The rate of forgetting can be captured by the corresponding decay constant of this function.
Considering that this decay constant is difficult to relate to the function image, we tend to transform this decay constant to obtain a fitting formula for the forgetting curve:
In this equation,
The relationship between
The notion of "memory stability,"
The two components of memory proposed by Bjork's - retrieval strength and storage strength - correspond precisely to recall probability and memory stability.
The equation embodies three distinct properties:
-
When
$t=0$ ,$R=100%$ , signifying that upon immediate review, the process of forgetting has not yet began, and the probability of recall reaches it's maximum value of 100%. -
As
$t$ approaches infinity,$R$ approaches zero, indicating that if you never review something, you will eventually forget it. -
The first derivative of the negative exponential function is diminishing, aligning with the empirical observation that forgetting is fast initially and slow down subsequently.
Thus, we have defined two main components of memory, but it seems like something's missing.
When the shape of the forgetting curve changes, the memory stability changes, and it doesn't depend only on the probability of recall at the time of the review and the previous value of memory stability.
Is there evidence to substantiate this claim? Think about the first time you learn something: your memory stability and probability of recall are both zero. But after you learn it, your probability of recall is 100%, and the memory stability depends on a certain property of the material you just learned.
Basically, the thing you're trying to remember itself has some features that can affect your memory. Intuitively, this variable is the difficulty of material.
With this variable of difficulty added, we now have a three component model of memory.
| Question | Answer |
|---|---|
| Why can't a single variable of memory strength adequately describe the state of memory? | A single variable is insufficient because the forgetting curve encompasses both retention levels and the rate of forgetting. |
| What variable measures the degree of memory retention? | Recall probability |
| Which function can approximate the forgetting curve? | Exponential function |
| What variable measures the speed of forgetting? | Decay constant |
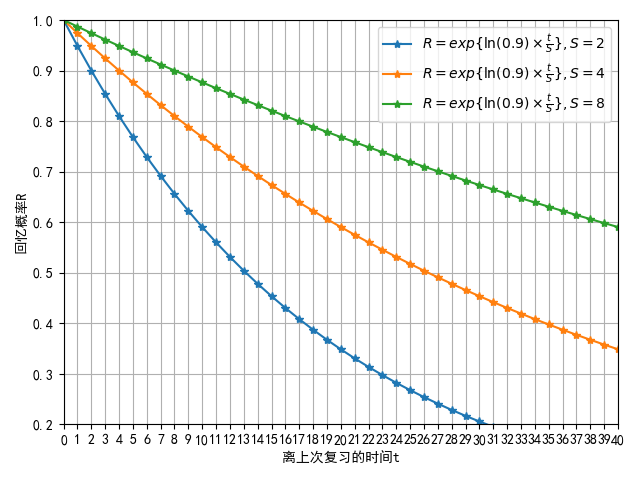
| What is the definition of memory stability? | The time required for the recall probability to decline from 100% to a predetermined percentage, often 90%. |
Let us delve directly into the terms:
- Stability: The duration required for the probability of recall for a particular memory to decline from 100% to 90%.
- Retrievability (probability of recall): The probability of recalling a specific memory at a given moment.
- Difficulty: The inherent complexity associated with a particular memory.
The difference between retrievability and retention is that the former refers to the probability of recalling a singular memory, whereas the latter refers to the average recall probability for a population of memories.
With above terms, one can define the retrievability of any given memory at time
By transforming
Where:
-
$I_1$ denotes the interval prior to the first review. -
$C_i$ represents the ratio between the$i$ -th review interval and the preceding$i-1$ -th review interval.
The objective of spaced repetition algorithms is to accurately compute
To recap, both SM-0 and SM-2 algorithms have an
The question is, what is the relationship between
One could ponder this by thinking how the state of memory updates during each review.
Below are some empirical observations from Woz, corroborated by data from vocabulary learning platforms like MaiMemo:
- Impact of stability: A higher
$S$ results in a smaller$C_i$ . This means that as memory becomes more stable, its subsequent stabilization becomes increasingly hard. - Impact of retrievability: A lower
$R$ results in a larger$C_i$ . This means that a successful recall at a low probability of recall leads to greater stability. - Impact of difficulty: A higher
$D$ results in a smaller$C_i$ . THis means that greater complexity of the material leads to a smaller increase in stability after each review.
Due to the multifarious factors at play,
For the sake of subsequent discourse, we shall adopt SM-17's naming for
Let us now delve into a more detailed discussion of stability increase.
| Question | Answer |
|---|---|
| Which variables are encapsulated in the three component model of memory? | Memory stability, memory retrievability, and memory difficulty. |
| What differentiates retrievability from retention rate? | The former pertains to individual memories, whereas the latter refers to large populations of memories. |
| What two values connect the three component model of memory and spaced repetition algorithms? | The initial review interval |
| What is |
Stability increase |
In this chapter, we momentarily set aside the influence of memory difficulty to focus on the intricate relationship between memory stability increase, stability, and retrievability.
Data for the following analysis is collected from SuperMemo users and scrutinized by Woz.
Upon investigating the stability increase (SInc) matrix, it became evident that for a given level of retrievability (R), the function of SInc with respect to stability (S) can be accurately approximated by a negative power function.
By taking the logarithm of both stability increase (Y-axis) and stability (X-axis), the following curve is attained:
This corroborates our prior qualitative conclusion, "As S increases,
As predicted by the spacing effect, stability Iincrease (SInc) is negatively correlated with retrievability (R); in other words, SInc is greater for lower values of R. After analyzing multiple datasets, it was observed that SInc demonstrates exponential growth as R diminishes.
Upon logarithmically transforming retrievability (X-axis), the following curve is achieved:
Surprisingly, SInc may fall below one when R is at 100%. Molecular-level research suggests an increase in memory instability during review sessions, thereby corroborating once more that rote repetition not only wastes time but also impairs memory.
As time (t) increases, eetrievability (R) exponentially diminishes, while Stability Increase (SInc) conversely exhibits an exponential ascent. These two exponents counterbalance each other, yielding an approximately linear trajectory.
Optimization of learning encompasses diverse benchmarks; one could tailor strategies for specific retention rates or aim to maximize memory stability. In either scenario, comprehending the anticipated stability increase proves advantageous.
We define the expected stability increase as:
This equation divulges a startling revelation: the apex of anticipated stability augmentation occurs when the retention rate resides between 30% and 40%.
It's crucial to note that maximal expected stability increase does not necessarily equate to the greatest speed of learning. For the most efficient review schedule, refer to the forthcoming SSP-MMC algorithm.
| Question | Answer |
|---|---|
| What mathematical function describes the relationship between stability increase and memory stability? | Negative power function |
| What mathematical function describes the relationship between stability increase and memory retrievability? | Exponential function |
Memory stability during spaced repetition depends on the quality of memory, termed here as memory complexity. For efficient review sessions, knowledge associations must remain simplistic — even if the knowledge itself is intricate. Flashcards can encapsulate complex knowledge architectures, yet individual flashcards ought to remain atomic.
In 2005, we formulated an equation to describe the review of composite memories. We observed that the stability of a composite memory behaves akin to resistance in a circuit; parallel resistance allows greater electrical current to pass through. (*Note: Composite is used in lieu of complex to emphasize its composed nature of simpler elements.)
Composite knowledge yields two primary conclusions:
- Additional information fragments lead to inteference
- Uniformly stimulating the sub-components of the memory during review is very difficult
Suppose we have a composite flashcard that requires the memorization of two fill-in-the-blank fields. Assume both blanks are equally challenging to remember. Hence, the retrievability of the composite memory is the product of the retrievabilities of its sub-memories.
Inserting this into the decay curve equation,
Here,
Leading to,
Remarkably, the stability of a composite memory will be lower than the stabilities of its constituent memories. Based on this conclusion, the stabilities of the two sub-memories will converge towards the stability of the more challenging sub-memory.
| Question | Answer |
|---|---|
| What is the relationship between the retrievability |
|
| Can the stability |
The stability of a composite memory is lower than the stabilities of its individual components. |
| How does the stability of a composite memory change as the number of its constituent memories increases? | It progressively diminishes, asymptotically approaching zero. |
After learning some theories of memory, it's time to put them into practice. The upcoming advancements will introduce how MaiMemo applies these memory theories, develops its own spaced repetition algorithms, and improves users' memory efficiency.
There will be no review section next, and the difficulty will increase sharply, so be prepared!
Data is the lifeblood of spaced repetition algorithms. Collecting appropriate, comprehensive, and accurate data will determine the limits of the capabilities of spaced repetition algorithms.
To accurately estrimate learner's memory states, we need to define the basic behavior of memory. Let's think about it: what are the important attributes of a memory behavior?
The most basic elements are easy to think of: who (the subject), when (time), and what (memory). For memory, we can further explore: what was remembered (content), how well it was remembered (response), and how long it took (time spent), etc.
Taking these attributes into consideration, we can use a tuple to record a memory behavior event:
This event records a user's response and cost for a particular item at a certain time. For example:
That is: Jarrett reviewed the word "apple" at 12:00:01 on April 1st, 2022, forgot it, and he spent 5 seconds reviewing this material.
With the basic definition of memory behavior events, we can extract and calculate more information of interest based on this foundation.
For example, in spaced repetition, the interval between two repetitions is essential information. Using the memory behavior events mentioned above, we can group event data by user and item, sort by time, and then subtract the time of two adjacent events to obtain the interval. Generally, to save calculation steps, the interval can be directly recorded in the event. Although this causes storage redundancy, it saves computational resources.
In addition to time intervals, the historical sequences of feedback and intervals are also important features. For example, "forgot, remembered, remembered, remembered" and "1 day, 3 days, 6 days, 10 days" can reflect a memory behavior's independent history more comprehensively and can be directly recorded in memory behavior events:
If you are interested in the data, you can download the open-source dataset from MaiMemo and analyze it yourself.
Now that we have the data, how can we use it? Reviewing the three component memory model from Day 2, what we want to know are the various attributes of memory states, which our current data collection does not include. Therefore, the goal of this section is to convert memory behavior data into memory states and their transition relationships.
The three letters in the DSR model correspond to difficulty, stability, and retrievability. Retrievability reflects the probability of recalling a memory at a certain moment. In probabilistic terms, memory behavior is a single random experiment with only two possible outcomes, and its success probability equals retrievability.
Therefore, the most straightforward method to measure retrievability is to perform countless independent experiments on the same memory and then count the frequency of successful recall. However, this method is infeasible in practice. Because experimenting with memory will change its state, we cannot act as an observer and measure memory without affecting it. (Note: at the current level of neuroscience, it is impossible to measure memory states at the neural level, so this approach is also unavailable for now.)
So, are we out of options? Currently, there are two compromise measurement methods: (1) Ignore the differences in the learning material: SuperMemo and Anki both belong to this category; (2) Ignore the differences between learners: MaiMemo belongs to this category. (Note: This has been considered now, but it was not when I started writing this paragraph. However, it does not matter, as it will not affect the understanding of the following section.)
Ignoring the differences in the learning material means that when measuring retrievability, we collect data with the same attributes except for the content that the user is learning. Although it is impossible to perform multiple independent experiments on one learner and one material, it can be done with one learner and multiple materials. On the other hand, ignoring the differences among learners involves collecting data from multiple learners with the same material.
Considering the sufficient amount of data in MaiMemo, this section will only introduce the measurement method that ignores learner differences. After ignoring them, we can aggregate to obtain a new group of memory behavior events:
Here, N is the number of learners who have memorized the same material and have the same historical behavior. Retrievability
After solving the retrievability issue, the stability can be easily calculated. Based on the collected data, an exponential function can be used to approximate this fata and calculate the stability of memory for groups with the same
The scatter plot coordinates are
Finally, it's time to tackle the difficulty. How can we derive the difficulty from memory data? Let's start with a simple thought experiment. Suppose a group of learners memorize the words "apple" and "accelerate" for the first time. How can we use memory behavior data to distinguish the difficulty of the two words?
The simplest method is to test immediately the next day, record the memory behavior data, and see which word has a higher proportion of successful recalls. Then we can calculate the corresponding value of stability.
That is to say, the stability after the first review can reflect the difficulty. However, there is no unified standard for using stability to estimate the difficulty. Since this is an introductory article, the problem of calculating difficulty will not be discussed in detail.
The rest of this article covers in-depth details about my research works. If you’re new to acdemics, you can stop here and review the content of the previous three days. If you’re interested in the following content, you can continue reading.
So far, we can transform memory behavior data into memory states:
Next, we can start describing the transition relationship between states. What is the relationship between
First, we still need to organize the memory state data into a form suitable for analysis:
Here,
In the end, the state transition data we need to analyze is as follows:
And
We can obtain the relationship formula (the influence of difficulty D is omitted here):
According to the above formula, we can predict the memory state
With the DSR memory model, we can simulate memory states under any review schedules. So, how should we simulate it specifically? We need to start from the perspective of how ordinary people use spaced repetition software in reality.
Suppose Jarrett needs to prepare for the GRE in four months and needs to use spaced repetition to memorize the English words in the exam syllabus. However, time must also be allocated to prepare for other subjects.
From the above sentence, there are two obvious constraints: the number of days before the deadline and daily learning time. The Spaced Repetition System (SRS) simulator needs to take these two constraints into consideration, and this also highlights the two dimensions of SRS simulation: by day and in day. In addition, the number of syllabus words is limited, so the SRS simulation also has a finite set of cards, from which learners select materials for learning and review every day. The arrangement of review tasks is managed by the spaced repetition scheduling algorithm. To sum up, SRS simulation requires:
- Material set
- Learner
- Scheduler
- Simulation duration (in day + by day)
The learner can be simulated using the DSR model, providing feedback and memory state for each review. The scheduler can be SM-2, Leitner System, or any other algorithm for scheduling reviews. The simulation duration and material set need to be set according to the situation to be simulated.
Then, we will design a specific simulation process based on the two dimensions of SRS simulation. Obviously, we need to simulate day by day into the future in chronological order, and the simulation of each day is composed of feedback from card by card. Therefore, the SRS simulation can consist of two loops: the outer loop represents the current simulated date, and the inner loop represents the current simulated card. In the inner loop, we need to specify the time spent on each review, and when the accumulated time exceeds the daily learning time limit, the loop is automatically exited, ready to enter the next day.
Here is the pseudocode for SRS Simulation:
The pertinent Python code has been open-sourced on GitHub for readers who are intrigued enough to delve into the source code: L-M-Sherlock/space_repetition_simulators: Spaced Repetition Simulators (github.com)
Having discussed the DSR model and SRS simulation, we can now predict learners' memory states and memory situations under given review schedules, but we still haven't answered our ultimate question: What kind of review schedules is the most efficient? How to find the optimal review schedule? The SSP-MMC algorithm solves this problem from the perspective of optimal control.
SSP-MMC is an acronym for Stochastic Shortest Path and Minimize Memorization Cost, encapsulating both the mathematical toolkit and the optimization objective underpinning the algorithm. The ensuing discourse is adapted from my graduate thesis, "Research on Review Scheduling Algorithms Based on LSTM and Spaced Repetition Models," and the conference paper A Stochastic Shortest Path Algorithm for Optimizing Spaced Repetition Scheduling.
The purpose of the spaced repetition method is to help learners form long-term memory efficiently. Whereas the memory stability measures the storage strength of long-term memory, the number of repetitions and the time spent per repetition reflect the cost of memory. Therefore, the goal of spaced repetition scheduling optimization can be formulated as either getting as much material as possible to reach the target stability within a given memory cost constraint or getting a certain amount of memorized material to reach the target stability at minimal memory cost. Among them, the latter problem can be simplified as how to make one memory material reach the target stability at the minimum memory cost (MMC).
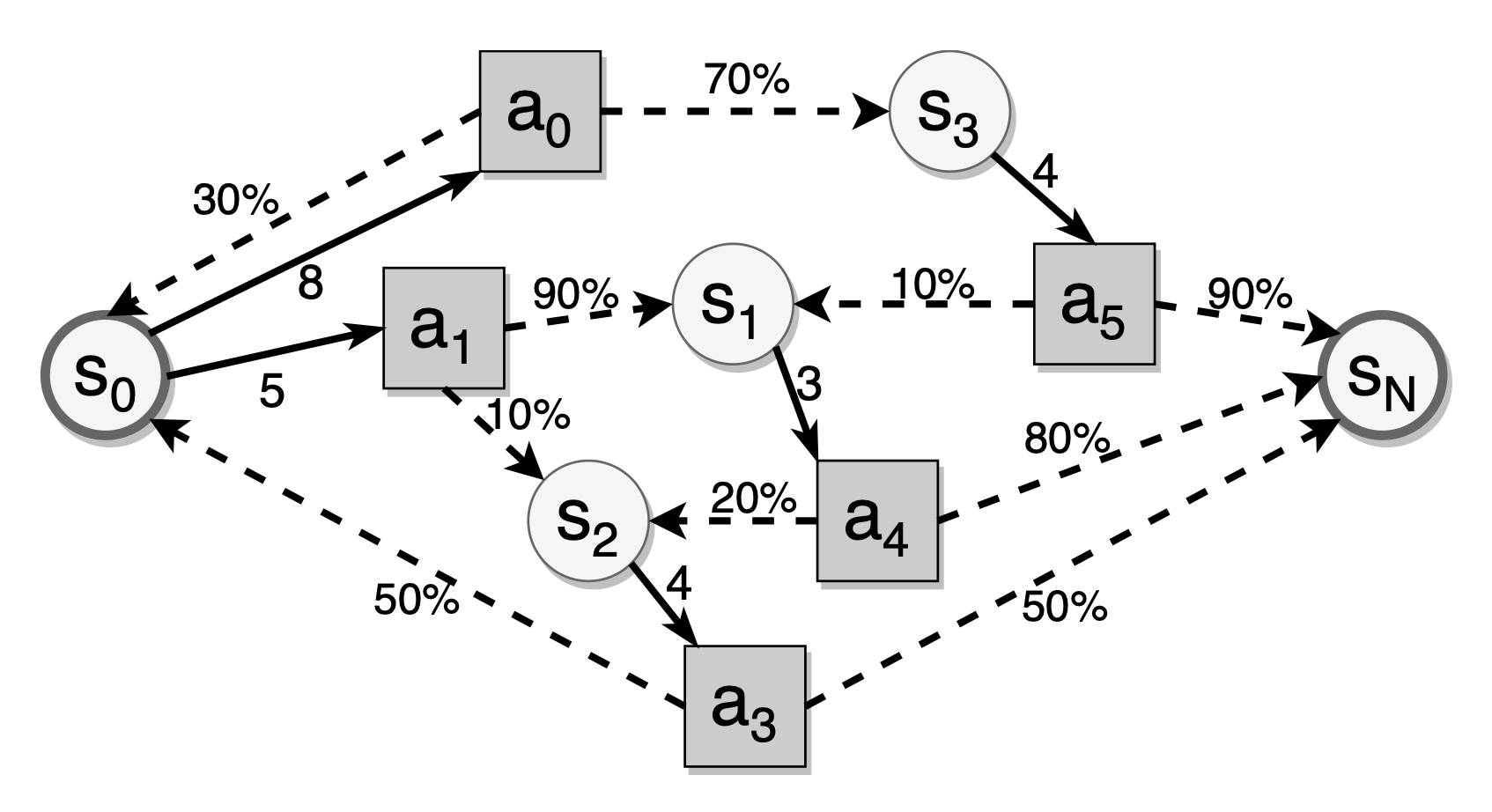
The DSR model satisfies the Markov property. In DSR model, the state of each memory depends only on the last stability, the difficulty, the current review interval, and the result of the recall, which follows a random distribution relying on the review interval. Due to the randomness of stability state-transition, the number of reviews required for mem- orizing material to reach the target stability is uncertain. Therefore, the spaced repetition scheduling problem can be regarded as an infinite-time stochastic dynamic programming problem. In the case of forming the long-term memory, the problem has a termination state which is the target stability. So it is a Stochastic Shortest Path (SSP) problem.
As shown in above figure, circles are memory states, squares are review action (i.e., the interval after the current review), dashed arrows indicate state transitions for a given review interval, and black edges represent review intervals avail- able in a given memory state. The stochastic shortest path problem in spaced repetition is to find the optimal review interval to minimize the expected review cost of reaching the target state.
To solve the problem, we can model the review process for each flashcard as a Markov Decision Process (MDP) with a set of states
$$ \begin{aligned} \pi^* = \arg\min_{\pi \in \Pi} \lim_{{N \to \infty}} \mathbb{E}{s{0}, a_{0}, \ldots} \left[ \sum_{t=0}^{N} \mathcal{J}(s_{t}, a_{t}) \mid \pi \right] \end{aligned} $$
The state-space
where the
We solve the Markov Decision Process
$$ \begin{aligned} \mathcal{J}^(s) &= \min_{a \in \mathcal{A}(s)} \left[ \sum_{s'} \mathcal{P}_{s,a}(s') \left( g(r) + \mathcal{J}^(s') \right) \right] \ s' &= \mathcal{F}(s,a,r,p) \end{aligned} $$
where the
Based on above Bellman equation, the Value Iteration algorithm uses a cost matrix to record the optimal cost and a policy matrix to save the optimal action for each state during the iteration.
Continuously iterate through each optional review interval for each memory state, compare the expected memory cost after selecting the current review interval with the memory cost in the cost matrix, and if the cost of the current review interval is lower, update the corresponding cost matrix and policy matrix. Eventually, the optimal intervals and costs for all memory states will converge.
In this way, we obtain the optimal review policy. Combined with the DSR model for predicting memory states, we can arrange the most efficient review schedule for each learner using the SSP-MMC algorithm.
This algorithm has been open-sourced in MaiMemo's GitHub repository: maimemo/SSP-MMC: A Stochastic Shortest Path Algorithm for Optimizing Spaced Repetition Scheduling (github.com). Readers interested in an in-depth examination are encouraged to fork a copy for local exploration.
Congratulations on reaching the end! If you haven't given up, you've already entered the world of spaced repetition algorithms!
You may still have many questions, some of which may have answers, but many more are unexplored areas.
My capacity to address these questions is decidedly limited, yet I am committed to dedicating a lifetime to advancing the frontiers of spaced repetition algorithms.
I invite you to join me in unraveling the mystery of memory. Are you willing to walk this path with me?
History of spaced repetition - supermemo.guru
Original link: https://l-m-sherlock.github.io/thoughts-memo/post/srs_algorithm_introduction/
My representative paper at ACMKDD: A Stochastic Shortest Path Algorithm for Optimizing Spaced Repetition Scheduling
My fantastic research experience on spaced repetition algorithm: How did I publish a paper in ACMKDD as an undergraduate?
The largest open-source dataset on spaced repetition with time-series features: open-spaced-repetition/FSRS-Anki-20k